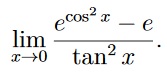Limita s funkcema

Ahoj, Jiří.

Použiji pro počítačem psaný text přijemnější označení, exp(x) čti jako e^x.

Řešení spočívá v tom, že hrajete na jednu z takových tabulkových limit, a to sice lim x->0 exp(x) -1)/x, tato limita jde k jedničce, ověřit můžete dosazením z lim x->0 sinx/x a součtových vzorců, nebo kousek snáze L'hospitalem.

Tedy potřebujeme vykřesat ze zadání něco ve tvaru lim x->0 (exp(x) -1)/x.

Funkci ze zadání můžeme přepsat pomocí vytknutí e-čka na tvar e*(exp(cos^2(x)-1) -1)/(sin^2(x)/cos^2(x)).

Dále využijeme vztahu, že sin^2(x)=1-cos^2(x), nebo spíše -sin^2(x)=cos^2(x)-1, což je funkce x, kterou máme v exponentu eulerova čísla v čitateli.

Ze jmenovatele tedy vytkneme -1, abychom získali onen zmíněný -sin^2(x) a převedli. V tomto kroku zpráskáme rovnou i vzniklý složený zlomek. Dostaneme

(-1)ecos^2(x)*(exp(cos^2(x)-1) -1)/(cos^2(x)-1/cos^2(x)), nyní můžeme udělat mazanou substituci v limitě.

Vidíme, že cos^2(x)-1 je funkce x, která když x jde k nule, jde také k nule (cos(1^2)-1 = 0).

Před provedením substituce ještě rozdělme limitu na součin dvou limit a to sice

(lim x->0 -ecos^2(x))(lim y->0 (exp(y)-1)/y), ke y(x) = cos^2(x)-1

(to je proveditelné díky tomu, že funkce jde také k nule když jde x k nule).

Substituovaná limita má výsledek = 1 (to už je ta tabulková, odvozená), čili dostáváme

1*(lim x->0 -e*cos^2(x)), tady už jen dosadíme a dostáváme výsledek, že

(exp(cos^2(x)) -e)/(tg^2(x)). = 1*(-e)*cos(1)^2, čili -e.

Je to srozumitelné?

Díky za čas,

Jan.

Ahoj, děkuji moc, už to chápu a moc mě to pomohlo.