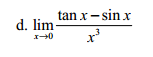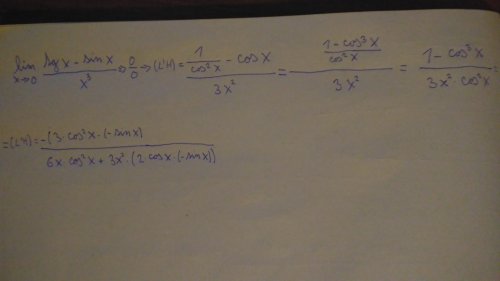Limita funkce
Zdravím přátelé,potřeboval bych pomoct s vyřešením jednéí limity.Není to nic složitého,ale už pěknou chvíli se snažím o vyřešení a furt se mi to nedaří. V goniometrických funkcích jsem vždycky plaval,zvlášť když jde teď o derivaci :-) (Výsledek má vyjít x=1/2.
Daniel K.
29. 12. 2016 22:15
6 odpovědí
Zapomněl jsem dodat,že to mám počítat pomocí L'Hospitala. :)
Ahoj Danieli, ideální by bylo, kdybys mohl poslat svůj postup (myslím vyfocený na papíře). Jinak je to typ 0/0, takže můžeme L'H použít, derivujeme čitatel a jmenovatel zvlášť.
Můj postup byl zhruba takovýhle :) Dál jsem nic nerozepisoval,protože předtím jsem zkošel x způsobů jak pokračovat,ale ani jeden nevedl ke správnému výsledku..Opět jsem derivoval L'H,ale jelikož tam bylo moc násobení tak jsem to asi popletl,nebo je nutná nějaká úprava podle goniometrických vzorců,které neovládám. Nějaká rada jak pustupovat dál,případně co je špatně? :) Děkuji.
Zderivované je to dobře, ale musíme tam neustále psát to lim(pro x jdoucí k 0). Ten poslední výraz nejdříve upravíme (jenom zkrátíme – čím?) a ověříme, že pro x = 0 je to zase typ 0/0 a znovu (nejspíše naposledy derivujeme).
Na to jsem zapomněl v té rychlosti :) Nevšiml jsem si,že můžeme vytknout cos x..poté upravíme,stále po ověření je to typ 0/0,použijeme opět L'H a nyní po dosazení už to vychází 1/2 jak to má být. Děkuji Martine za popostrčení a především za ochotu pomoct! :-)
Přesně tak a není zač :-) Mimochodem i bez toho zkrácení je to samozřejmě stále typ 0/0 a můžeme použít L'H, ale byly by tam složitější derivace, především asi to 3x^22cos(x)(–sin(x)), tj. součin 3 funkcí, ale jako procvičení v derivacích to rozhodně není špatné, doporučuji :-)
P.S. Po prouzkoumání se ukáže, že je to také součin dvou funkcí, protože platí 2*sin(x)cos(x) = sin(2x) :-)