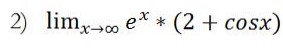Limita pro X jdoucí k nekonečnu

Ahoj Moniko,nerad bych ti poradil špatně,nicméně zatím nikdo nezareagoval a tak se pokusím pomoct.

Limita ''e˛na x'' když x->nekonečno = nekonečno. Limitu cos x v nekonečnu nemůžeme přesně určit.Nicméně vycházíme z toho,že funkční hodnoty cos x jsou omezeny na interval <-1,1>. Takže i kdybychom uvažovali cos x v nekonečnu bude lokálním extrémem,tudíž -1 nebo +1,tak výraz v závorce bude buď max (2+1)=3 nebo 2+(-1)=1 ..ale pořád to bude kladné. Takže Nekonečno * kladné číslo =nekonečno..

Druhá možnost je,že limita nebude definována právě z toho důvodu,že lim x->nekonečno z cos x se nedá přesně určit.

Ber to spíš jako takovou úvahu než správné řešení,nejsem si tím tak jistý :) pokud je to špatně,prosím někoho povolanějšího,aby mě opravil :)

Danieli, myslíš to správně, jenom špatně argumentuješ.

e^x v nekonečnu diverguje do nekonečna. 2+cosx v nekonečnu nekonverguje, ale osciluje.

Pak je potřeba vyjít z definice limity a dokázat odhad, že celá limita diverguje k nekonečnu.

Pokud pro libovolné reálné K>0 dokážeš najít X0 takové, že pro x>X0 platí e^x*(2+cosx) > K, bude důkaz hotový.

Platí: e^x*(2+cosx) >= e^xinf{ 2+cosx} = e^x1 = e^x > K

Pro zvolené K tedy postavíme X0 = ln(K) a máme důkaz divergence.