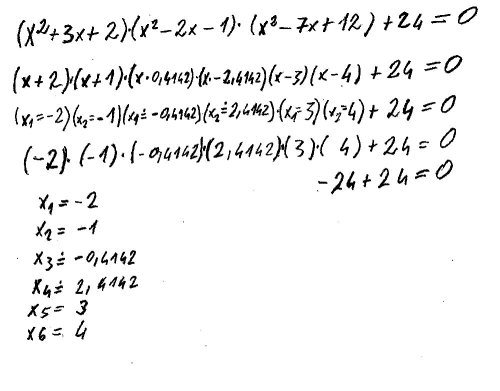Zajímavá úloha: Sextická rovnice

Zdravím,

zkusil jsem to vyřešit,ale nevím jestli to jde tímto způsobem. Pavel

Ahoj Pavle,takhle by to šlo jen v případě,kdybys tam neměl +24,jinak ti to nevýjde,tys určil nulové body závorek,takže se celý ten součin bude rovnat 0 a to znamená,že bys měl 24=0.

Jojo, je to přesně tak jak píše Vladan. K tomu prvnímu řádku jsem se taky dostal, ale tím jsem skončil :-)

A ještě jsem si Pavle všiml jedné věci...x může v jednom okamžiku nabývat pouze jedné hodnoty. Ten čtvrtý řádek je roven nule, ale nevím jak jste se k němu dostal...protože pokud by x byly pro každou tu závorku jiní, takové jak píšete v řádku 3, tak by ty závorky byly nulové...

Nápověda: Možná jste si všimli, že součin absolutních členů u oněch třech kvadratických členů je -24, můžete to tedy zkusit roznásobit a poté "pouze" řešit kvintickou rovnici (po vytknutí x) NEBO zkusit najít vhodnou SUBSTITUCI. K této substituci mohu říct pouze toto: kam se na to hrabou sebetěžší integrály - pokud se u integrálů říká že se kouzlí, tak tady co je to potom tady :-) Vtip je v tom rozložit první a třetí kvadratický trojčlen a zkusit to nějak "nakombinovat" (hledat shodu s tím prostředním). Hodně štěstí všem odvážlivcům! :-)

P.S. Přeji Mistrovi vše nejlepší k svátku! :D

Ahoj,po dlouhým přemlouvání sama sebe jsem se do toho pustil (nemusím obrovské násobení).Nejprve jsem odhadl dva kořeny,x=0 a x=2,roznásobil jsem to,vydělil (x-2),tím jsem dostal to dokázal převéct na tvar x(x-2)(x^4-4x^3-8x^2+24x+35)=0 a to se dá zapsat ve tvaru : x(x-2)(ax^2+bx+c)(dx^2+ex+f) a přitom musí platit následující : b+e=-4 (koecifient před x^3) , fc=35 (absolutní člen) a=1,d=1 (protože koecifient před x^4 je 1),pak ce+fb=24 (linearní člen) a nakonec musí ještě platit be+af+cd=-8 , řídil jsem se jen podle b+e=-4 a f*c=35 (pak jsem musel zkontrolovat samozřejmě i jestli platí ostatní vztahy) po chvilce koukání jsem došel k tomu,že b=-2,e=-2 (řídil jsem se podle toho,jaké hodnoty by byly nejpravděpodobnější(moc toho na výběr ani nebylo,počítal jsem s tím,že nás snad nebudou trápit se zlomkama)) f=-5,c=-7 a tím jsem určil všechny koecifenty,které potřebujeme,takže jsem to dokázal převést do tvaru x(x-2)(x^2-2x-7)(x^2-2x-5)=0.Vyřešil jsem kvadratickou rovnici x^2-2x-7=0 a x^2-2x-5=0 a tím jsem došel k dalším čtyřem kořenům.Takže nakonec mám kořeny (snažil jsem se je dostat do co nejkrásnějšího tvaru) : x1=0 , x2=2, x3=1-2√2 , x4=1+2√2 , x5=1+√6 , x6=1-√6 .

Doufám,že jsem neudělal numerickou chybu,násobit to bylo docela zdlouhavý a pak se v tom hlavně neztratit. :) Tak mi dej vědět,jestli je to dobře (dělat zkoušku pro x3,x4,x5,x6 mě teda moc neláká).

Jinak by se dalo dostat do obdobnýho tvaru tím,že bych si rozložil (x^2+3x+2)(x^2-2x-1)(x^2-7x+12)+24=0 na : (x-3)(x-4)(x+2)(x+1)(x^2-2x-1)+24=0 , teď vynásobil x-3 s x+1 a x-4 s x+2 ,protože jak ten první,tak ten druhý součin mi dá u linearního členu stejný koecifient,takže to dokážu dostat do tvaru : (x^2-2x-1)(x^2-2x-3)(x^2-2x-8)+24=0.Teď použiju substituci a=x^2-2x a tím pádem to dokážu převést do tvaru : (a-1)(a-3)(a-8)+24=0 ,roznásobím to a dostanu : a^3-12a^2+35a=0,vytknu "a" a rovnice bude vypadat následovně : a(a^2-12a+35)=0 ,takže mám a=0 a pak a^2-12a+35=0,to rozložím na (a-5)(a-7),dostávám a=5 a a=7 , zpětně dosadím za "a" a tím zjistím kořeny,v prvním případě to je x^2-2x=0 ---> x1=0 a x2=2 a dále mám : x^2-2x-5=0,z toho zjistím kořeny x3=1+√6 a x4=1-√6 a z poslední rovnice : x^2-2x-7=0 ---> x5=1+2√2 , x6=1-2√2.

Bravo! :-)