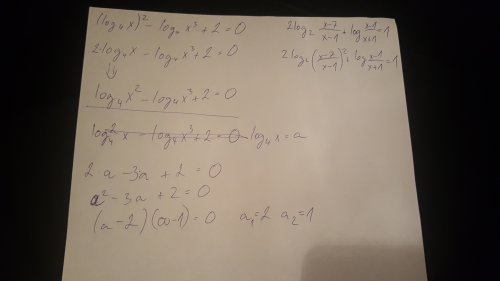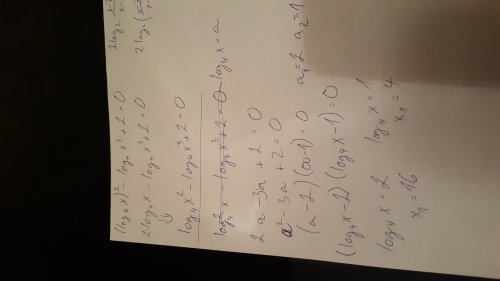Rovnice

Ahoj Nikolo,

ve 4. řádku odečítáš 9q +18, tedy –9q–18, ale to by na pravé straně zbylo něco jiného, než 0. Např. –5x – 5x = –10x, nikoli 0.

Jojo, už to vidím, děkuju.

Zdravím som tu dnes 1. krát tak ma prosím šetrite. Rád by som sa spýtal či je vrchný príklad č.7 vypočítaný správne- dúfam že áno.

A hlavne kde je chyba v spodnom príklade č.2? Po z bežnej skúške vpravo mi to nesedí.

Vďaka.

Ahoj Milane, myslím, že bude lepší, když příště položíš "nový dotaz", aby se to nepletlo. Příklad 7: celý logaritmus umocněný na nějaké číslo (tady na druhou) zapisujeme jinak, viz https://www.google.cz/search?q=logaritmus+na+druhou…:

A pokud je to skutečně druhá mocnina celého logaritmu, tak rozhodně nemůže mocninu přesunout nad logaritmované číslo (argument).

Příklad 2: Kolik je 2^3 krát 2^2? Když správně odpovíš na tohle, objevíš i chybu ve tvém příkladě.

Ďakujem za rýchlu odpoveď. Áno v č. 2 sa násobenie sčitava....som jelito.

Akurát som nepochopil v príklade č. 7 keď je celý logaritmus na druhú tak ako sa odstránia zátvorky? Nenašiel som to ani na videách o logaritmoch a akosi ani z linku nechápem..

Do budúcnosti urobím teda nový dotaz. Nevedel som ako to tu funguje.

Nic se nestalo. Když je logaritmus na druhou, tak se tam ty závorky nepíší a píše se ta dvojka nad log, tak jak je na tom obrázku, co jsem poslal. Další řešení tkví v zavedení substituce log_4(x) = a (to "_4" značí dolní index- základ logaritmu). Ještě je potřeba využít pravidla, že mocninu logaritmovaného čísla (výrazu) může vytknout před logaritmus, např. log(10^2) = 2 krát log(10).

No ale ako to mam počítať keď je nad log ta 2ka? Na žiadnom videu som podobný príklad aby celý logaritmus bol mocneny nenašiel. Iba keď je pred logaritmov číslo. A to sa potom da ako mocnina log. čísla.

Nemôžte mi ten príklad vypočítať a odfotit aby som pochopil postup?

Zavedeme tu substituci log_4 (x) = a, log na druhou se pak bude rovnat a^2. V tom druhém logaritmu vyhodíme 3 před log a budem tam mít –3krát ten log, tedy –3a (minus tam už bylo), s dvojkou se nic nestane. Pro "a" nám vznikne rovnice a^2 – 3x + 2 = 0. Tu vyřešíme a zpátky dosadíme do té substituce, abychom zjistili x.

Takto nejak? No ale aj tak, potom ako ďalej? Čo mám dať naspäť za ten vyraz log4x? Nechápem...

Vlastně jsme to rozložili na součin (nepíšu tam ten základ 4): (a-2)(a-1)=0 , ale "a" = log(x), takže (log(x) – 2)(log(x) – 1) = 0 => => => a = 2 nebo a = 1, tedy log(x) = 2 nebo log(x) = 1. Z toho dopočítáme x.

Super. Ďakujem za rady. A som rád že ste ma naviedol na to a nie ze ste to hneď napísal...

Takže výsledky sú 16 a 4?

Není zač, jsem moc rád, že to píšeš. Matematika by se podle mě měla objevovat, tak jí člověk porozumí nesrovnatelně rychleji a dá mu to mnohem víc. Jinak přesně tak, řešením jsou čísla 4 a 16. To, že vyšla 16 i po špatném postupu je jen náhoda :-)