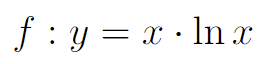Asymptota
Dobrý den, vyšetřuje průběh této funkce a chci vypočítat asymptotu. Podle vzorečku y=kx+q
Jenomže k mi vychází +nekonečno.
Spočítal jsem limitu špatně nebo jaký by teď měl být postup?
Moc děkuji za každou odpověď
Lukáš K.
12. 12. 2020 11:40
4 odpovědi
Zdravím,
hledáme asymptotu se směrnicí - a směrnice přímky nemůže být nekonečná. Tedy, když při výpočtu směrnice \( k \) pomocí limity vyjde nekonečno, graf asymptotu se směrnicí nemá.
V tomto případě pro \( x\rightarrow\infty \) vychází
\( k=\lim\frac{ f(x)} { x} =\lim\ln(x)=\infty\)
Děkuji, tedy má pouze asymptotu bez směrnice, která se rovná 0
Funkce nemá ani asymptotu bez směrnice.
Asymptota bez směrnice je svislá přímka, k níž se graf funkce neomezeně blíží (nahoru nebo dolů).
Přímka \( x=x_0 \) je asymptota bez směrnice, když má funkce v bodě \( x_0 \) některou jednostrannou limitu nevlastní (tj. nekonečnou).
Naše funkce má v bodě \( x=0 \) limitu zprava rovnu nule. Je to typ limity \( 0/\infty \), který převedeme např. na typ \( 0/0 \), viz např.
OPRAVA:
Je to typ limity \( 0\cdot (-\infty) \), který převedeme na typ \( 0/0 \).