Funkce s absolutní hodnotou a definiční obor

Příklad 3

Ve jmenovateli nemůže být nula, podmínky jsou dvě: $3x+4 \neq 0$, $x-4 \neq 0$ neboli

$x \neq -\frac{ 4} { 3}$, $x \neq 4$.

Definiční obor tvoří všechna reálná čísla kromě těchto dvou, např.:

$D(f)=(-\infty; -\frac{ 4} { 3} )\cup (-\frac{ 4} { 3} ; 4)\cup(4;+\infty)$

Příklad 4

Pod odmocninou musí být kladné číslo nebo nula. Pro první odmocninu je podmínka

$\displaystyle\frac{ 3x-2} { 1-x^2} \geq 0$

Zlomek je kladný (nebo roven nule), když čitatel i jmenovatel jsou kladná čísla (čitatel též roven nule):

$(3x-2\geq 0)\wedge (1-x^2>0)$

anebo když čitatel i jmenovatel jsou záporná čísla (čitatel též roven nule):

$(3x-2\leq 0)\wedge (1-x^2<0)$

První soustava nerovnic má řešení $\langle\frac{ 2} { 3} , +\infty)\cap (-1,1) =\langle\frac{ 2} { 3} ,1)$.

Pozn.: Nerovnici $1-x^2>0$ řešíme např. tak, že ji upravíme na $x^2<1$, řešením jsou všechna čísla, jejichž druhá mocnina je menší než 1, tedy $(-1,1)$.

V druhé soustavě má 1. nerovnice řešení $(-\infty,\frac{ 2} { 3} \rangle$, druhá $(-\infty,-1)\cup(1,+\infty)$, jejich průnik je $(-\infty,-1 )$.

Definiční obor první odmocniny je $(-\infty,-1 )\cup \langle\frac{ 2} { 3} ,1)$.

Pro druhou odmocninu platí podmínka

$\displaystyle\frac{ x^2+1} { x^2+9} \geq 0$

ale čitatel je vždy kladný, protože $x^2\geq 0$, tedy $x^2+1> 0$, podobně jmenovatel $x^2+9> 0$. Definiční obor této odmocniny proto tvoří všechna reálná čísla.

Definiční obor celé funkce je tedy $(-\infty,-1 )\cup \langle\frac{ 2} { 3} ,1)$.

Super trošku mi to osvěžilo paměť takže takhle je to správné??

Už se do toho dostávám doufám

Je to tak??

Příklad 1

Výsledek je dobře, ale nevidím postup :) Jde o funkci s absolutní hodnotou. Postupujeme obvykle přes "nulové body". Pro každý interval zapíšeme funkci zvlášť (odstraníme absolutní hodnoty).

Zde jsou nulové body $-10, +10$, které rozdělí osu $x$ na tři intervaly.

Postup ukážu třeba na prostředním intervalu $(-10, +10 )$. Do absolutních hodnot dosadím libovolné číslo z intervalu, např. $0$. V první absolutní hodnotě dostanu kladné číslo (při odstranění abs. hodnoty se výraz nezmění), v druhé záporné číslo (při odstranění abs. hodnoty se výraz změní v opačný).

$y=-3(x+10)+2(-x+10) +x-1= -4x-11$

To je ta "prostřední" část grafu, kde je funkce klesající.

Obdobně ve zbývajících dvou intervalech.

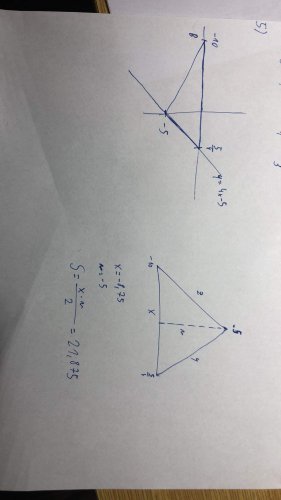
Příklad 5

Náčrtek je správně. Výpočet obsahu trojúhelníku: základna je $x=10+5/4=11.25$, výška $v=5$.

Příklad 3

Úprava je dobře. Definiční obor lze stanovit již z tvaru $(x-4)(3x+4) \neq 0$. Nemá-li se součin rovnat nule, nerovná se nule ani jeden z činitelů, tedy $x-4 \neq 0$, $3x+4 \neq 0$, odkud máme hned výsledky.