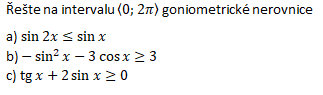Goniometrické nerovnice
Po urputném souboji s těmito nerovnicemi jsem došla k závěru že potřebuji pomoc místních chytrých hlav. U první rovnice jsem došla k závěru <π/3,π>u<5/3π,2π> ale vůbec si nejsem jistá správností svého postupu a natož potom výsledku. Proto bych vás ráda požádala o pomoc s řešením těchto nerovnic a o vysvětlení postupu.
Předem děkuji za pomoc! :)
Míša H.
01. 12. 2020 10:08
4 odpovědi
c) Tangens bych rozepsal pomocí sin, cos a postupnými kroky upravil na součinový tvar
\( \tan(x) (1+2\cos(x)) \geq 0 \).
Tedy buď \( \tan(x) \geq 0 \) a zároveň \( 1+2\cos(x) \geq 0 \),
nebo \( \tan(x) \leq 0 \) a zároveň \( 1+2\cos(x) \leq 0 \).
Dále pomocí grafů, druhá nerovnice se ještě upraví.
b) Číslo 3 na pravé straně nerovnice lze upravit jako
\( 3=4-1= 4-[(\sin(x))^2+(\cos(x))^2]\).
Dostaneme kvadratickou nerovnici pro \( \cos(x) \), použijeme substituci \( \cos(x)=y \).
a) Použij vzorec pro \( \sin(2x) \) a pak uprav na součinový tvar.
Bude-li ještě z toho něco nejasného, napiš :)
Výsledek a) je dobře, postup:
\( 2\sin(x)\cos(x) \leq \sin(x) \)
\( 2\sin(x)\cos(x)-\sin(x) \leq 0 \)
\( \sin(x)[2\cos(x)-1] \leq 0 \)
Součin dvou činitelů je záporný (nebo nula), když je jeden z nich kladný (nebo nula) a druhý naopak záporný (nebo nula), tedy
\( \sin(x) \leq 0 \) a zároveň \( 2\cos(x)-1 \geq 0 \)
nebo
\( \sin(x) \geq 0 \) a zároveň \( 2\cos(x)-1 \leq 0 \).
Kosinus upravíme:
\( \sin(x) \leq 0 \) a zároveň \( \cos(x) \geq 1/2 \)
nebo
\( \sin(x) \geq 0 \) a zároveň \( \cos(x) \leq 1/2 \).
Sinus je kladný v 1. kvadrantu, záporný ve druhém.
Jak se řeší nerovnice s kosinem, viz např. příklad 1 zde (jen tam nebude \( +2k\pi \), protože v zadání je pouze interval od \( 0 \) do \( +2\pi \):