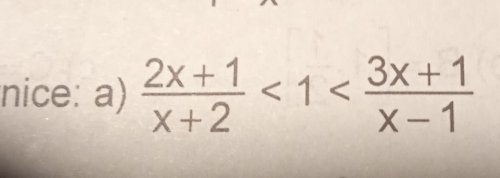Lineární nerovnice

Vlastně tam máte napsány tři funkce, yA

Máte tři funkce: aY,yB,yC, nakreslete si nejprve jejich asymptoty, jsou tu vždycky dvě, pak grafy, yA,yC dá hyperboly, yB dá přímku y=1. Z toho pak hned uvidíte, pro který interval x to platí, čili musí platit yA< yB, dále yA

Nechápu, proč to nedokáže vzít celý text, dále yA< yC a také yB

yB

yB< yC .

Nebo bez kreslení grafů:

Zadání nám definuje 3 rovnice. Průnik jejich řešení je výsledné řešení.

Nejprve podmínky - jmenovatel nesmí být nula: \(x \neq -2\) z prvního výrazu a \(x \neq 1\) z třetího.

První rovnice: \(\frac{ 2x+1} { x+2} < 1\), tedy \(\frac{ x-1} { x+2} < 0\). Zlomek je záporný, pokud se znaménko čitatele a jmenovatel liší, tedy \(x-1 > 0\) a \(x+2 < 0\) nebo \(x-1 <0\) a \(x+2 >0\).

První dvojice dá práznou množinu, druhá dvojice nám dá \(x \in (-2,1)\)

Druhá rovnice: \(1 < \frac{ 3x+1} { x-1} \), tedy \(0 < \frac{ 2(x+1)} { x-1} \), Zlomek je kladný, pokud má čitatel i jmenovatel stejné znaménko, tedy \(x+1 > 0\) a \(x-1 >0\) nebo \(x+1 < 0\) a \(x-1 <0\).

První dvojice dá \(x in (1;\infty)\), druhá pak \(x \in (-\infty,-1)\).

Průnik řešení prvních dvou rovnic dá \(x \in (-2,-1)\). Splnění těchto dvou rovnic přímo implikuje splnění třetí, takže tady můžeme přestat.

Pro kontrolu můžeme dopočítat i třetí rovnici: \(\frac{ 2x+1} { x+2} < \frac{ 3x+1} { x-1} \), tedy \(0 < \frac{ x^2+8x+3} { x^2+x-2} \).

Chceme stejná znaménka. Kořeny čitatele jsou \(-4 \pm \sqrt{ 13} \approx -7.5\) a \(-0.5\) a záporný je mezi nimi. Kořeny jmenovatele jsou \(-2\) a \(1\) a záporný je mezi nimi. Vidíme, že na výsledném intervalu \((-2,-1)\) jsou oba záporní a tedy je nerovnice splněna.