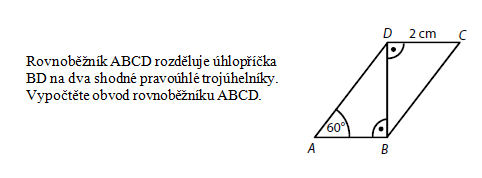
Obvody a obsahy

Z definice tangens máš \(\frac{ |BD|} { 2} =\tan60^\circ\)

Určíš |BD|. Pak z Pythagorovy věty dopočítáš |BC| a je to.

Dokonce by šlo spočítat rovnou |AD| ( nebo |BC| ), jestli si nepletu.

cos(60°) = 2/|AD| |AD| = 2/cos(60°) = 4

Omlouvám se za úpravu

[cos(60^{ \circ} )=\frac{ 2} { \left | AD \right |} ]

[\left | AD \right |=\frac{ 2} { cos(60^{ \circ} )} ]

[\left | AD \right |=4]

Snad už to bude v pořádku.

[cos(60^{ \circ} )=\frac{ 2} { \left | AD \right |} ]

[\left | AD \right |=\frac{ 2} { cos(60^{ \circ} )} ]

[\left | AD \right |=4]

Já budu doufat, že je to pochopitelné z prvního komentáře. :) Omlouvám se za spam.

Jen jsem se chtěl zeptat proč je tam |BD|/2 a ne jenom |BD|

děkuji za odpověď

Protože "tangens=protilehlá ku přilehlé" a přilehlá odvěsna je |AB|=2