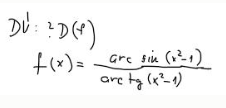Definiční obor u cyklometrické funkce
Dobry den, prosim o radu jak urcit definicni obor teto funkce?
\(f ( x ) = \frac { \arcsin ( x ^ { 2 } - 1 ) } { \operatorname { arctg } ( x ^ { 2 } - 1 ) } \)
Myslim ze definicni obor arcsin je <-1;1> a arctg by mel byt R, ale nevim presne jak to dat dohromady u tohoto prikladu.
Moc dekuji za rady
Steph R.
14. 10. 2020 15:38
5 odpovědí
\(\begin{ cases} -1\le x^2-1\le1\ \operatorname { arctg } ( x ^ { 2 } - 1 )\ne 0\end{ cases} \)
Jasny tohle mi vyslo taky,
takze definicni obor funkce f je
D(f)= <-1;0) U (0;1> ?
Dekuji
To asi ne. Jaké řešení má nerovnice \(-1\le x^2-1\ge1\) ?
Takže asi takhle?
0=<x=<2
zaroven teda x-1 se nesmí rovnat 0, takže
x se nesmí rovnat 1
takze asi takhle?
D(f) = <0;1)U(1;2 > ?
dekuji
Pořád to není dobře,
\(D_f=\langle-\sqrt2;-1)\cup(-1;1)\cup(1;\sqrt2\rangle\)