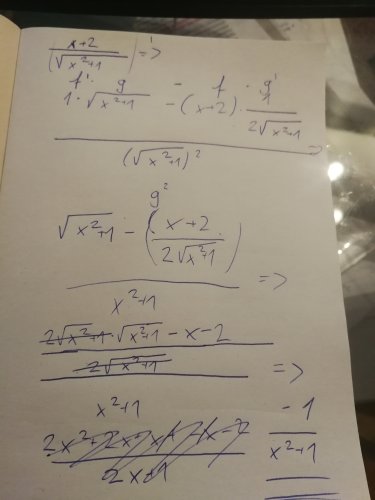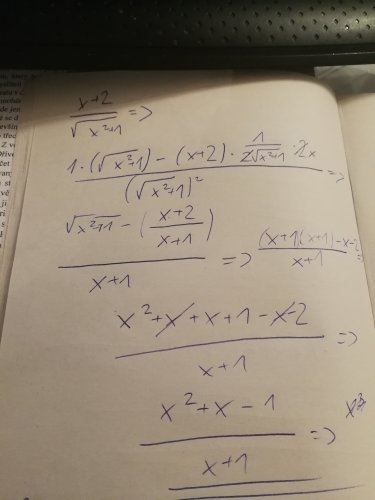Derivace podilu funkce 2

Výraz označený jako \(g' \) je potřeba ještě násobit derivací vnitřní funkce neboli

\( \displaystyle(\sqrt{ x^2+1} )' =\frac{ 1} { 2\sqrt{ x^2+1} } \cdot 2x=\frac{ 2x} { 2\sqrt{ x^2+1} } \)

Jedná se o složenou funkci, derivace vnitřní funkce je \( (x^2+1)' =2x \). Stačí takto?

Ahoj Robin, vyšlo mi to takto, je to správne? A dá sa to ješte nejak upravit ? Vopred dik, Katka

První řádek je dobře, ale kam se hned potom ztratila odmocnina z druhého členu v čitateli? :)

Výraz v čitateli bych upravil na společného jmenovatele, kterým bude právě ta odmocnina.

Ahoj, z tej odmocniny som udelala 2*(x+1) a danú 2 som pak skrátila. Zabudla som ale vynásobiť s x na konci riadku . Takže som to vynásobila s daným x a vyšlo mi x+1-[(x²+2x) / x+1] = (x+1)²-x²-2x / x+1 =1/x+1, je to tak?

Čitatele upravíme takto:

\(\displaystyle\sqrt{ x^2+1} -(x+2)\frac{ 1} { \sqrt{ x^2+1} } \cdot x=\sqrt{ x^2+1} -\frac{ x(x+2)} { \sqrt{ x^2+1} } \)

dále upravíme na společného jmenovatele

\(\displaystyle=\frac{ \sqrt{ x^2+1} \cdot\sqrt{ x^2+1} -x(x+2)} { \sqrt{ x^2+1} } \)

po úpravě

\(\displaystyle=\frac{ x^2+1-x(x+2)} { \sqrt{ x^2+1} } =\frac{ x^2+1-x^2-2x} { \sqrt{ x^2+1} } \)

ještě upravit "nahoře"

To jsme upravili čitatele - a výsledek nakonec dělíme jmenovatelem \( x^2+1 \) neboli násobíme \(\frac{ 1} { x^2+1} \).

Aha, ve jmenovateli je také chybička, má být

\(( \sqrt{ x^2+1} )^2=x^2+1 \)