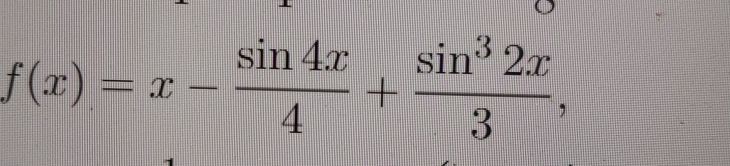Jak na derivaci goniometrických funkcí

Výsledek má být 16sinx na 2 x cosx na 4 x..

Ahoj, jde o derivaci složených funkcí, dle definice tedy $\frac{ d} { dx} f(g(x)) = \frac{ df} { dx} (g(x))\cdot \frac{ dg} { dx} (x)$. Při hlubším složení se to řetězí. V našem případě tedy:

$\frac{ d} { dx} \left(x - \frac{ \sin 4x} { 4} + \frac{ \sin^3 2x} { 3} \right) =$

$1 \left\lbrace\frac{ d} { dx} x = 1 \right\rbrace$

$- \frac{ 1} { 4} \cos(4x)\cdot 4\ \left\lbrace \frac{ d} { dx} \sin(x) = \cos(x)\text{ a } \frac{ d} { dx} 4x = 4\right\rbrace$

$+ \frac{ 1} { 3} \cdot 3\sin^2(2x)\cdot \cos(2x) \cdot 2 \left\lbrace \frac{ d} { dx} x^3 = 3x^2 \text{ a } \frac{ d} { dx} \sin(x) = \cos(x) \text{ a } \frac{ d} { dx} 2x = 2 \right\rbrace$

$= 1 - \cos 4x + 2\sin^2(2x)\cos(2x)$

Pak se asi dá hrát s vzorci, aby se člověk dostal na pouze "x" v argumentech.

Děkuji moc za odpověď :)