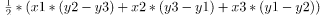Jak zjistit ze tří bodů zda se jedná o trojúhelník
Zdravím,
Sekl jsem se s problémem jak ze zadaných bodů určit zda je možné sestrojit trojúhelník. Body jsou zadávány pozicí v kartézské soustavě souřadnic (souřadnicová soustava „0xy“ – rovině).
Například - P1[1, 5], P2[2, 5], P3[4, 6]
Našel jsem vzorec viz příloha. Je opravdu takto možné zjistit zda se jedná o trojúhelník? Samozřejmě se mohu tento vzorec naučit nazpaměť, ale byl bych rád kdybych chápal jeho logiku.
Existuje ještě nějaky jednodušší vzorec na tuto problematiku?
Snad jsem mojí otázku popsal srozumitělně.
Děkuji všem za popřípadnou radu.
Jiří N.
22. 10. 2022 00:20
2 odpovědi
Zdravím,
\(\dfrac{ y_2-y_1} { x_2-x_1} =\dfrac{ y_3-y_1} { x_3-x_1} \)
Můžeš použít tuto rovnici. Když platí, body leží na přímce (a tedy netvoří trojúhelník), pokud neplatí, je to trojúhelník.
Pokud by ti někde ve jmenovateli vycházela nula, tak rovnici převrať a počítej \(\dfrac{ \Delta x} { \Delta y} \)
Jirko, vsechny tyhle vzorce jsou k nicemu, kdyz nechapes jak vznikly. Nejjednoduzsi test jestli je to trojuhelnik je, ze udelas z tech tri bodu dva vektory. Treba vektor AB a vektor AC. Pokud jsou rovnobezne, tak ty body lezi na primce a neni to trojuhelnik. Pokud nejsou rovnobezne, tak je to trojuhelnik. Rovnobeznost se pozna ze jeden vektor ne nasobkem druheho.