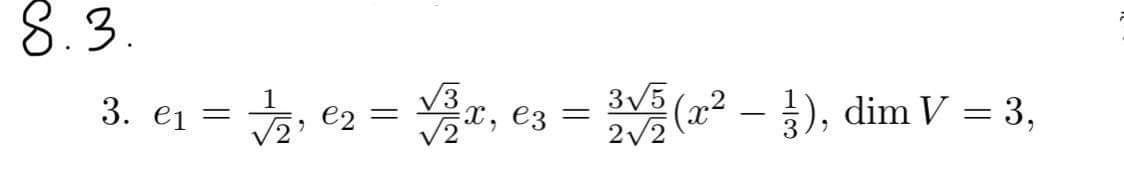Linearni algebra a hledání ortonormani báze pomoci integrálu

Do komentáře přikladám výsledek pro kontrolu

Ahoj Dominiku,

abys mohl určovat úhly a délky, potřebuješ unitární prostor. V zadání jsi dostal vektorový prostor \( V \) polynomů druhého stupně (tudíž \( dim V=3 \) ) a vnitřní produkt \( (u,v) \) definovaný Riemannovým integrálem, takže podmínky jsou splněny.

Vezmeš si libovolnou bázi prostoru \( V \), například \( v=(1, x, x^2) \) a dál použiješ Gram-Schmidtovu ortogonalizaci, přes kterou vytvoříš z báze \( v \) ortonormální bázi \( e \)

Spočítat \( e_1 \) je snadné, takže ukážu \( e_2 \) - nejdřív najdu vektor \( w_2 \), který je ortogonální k \( e_1 \) a pak ho upravím, aby jeho norma byla rovna jedné.

\( w_2 = v_2 - (v_2, e_1) = x - \int_{ -1} ^{ 1} x \frac{ 1} { \sqrt{ 2} } dx = x - 0 = x \)

\( (w_2, w_2) = \int_{ -1} ^{ 1} x.x.dx = \frac{ 2} { 3} \)

\( e_2 = \frac{ w_2} { \sqrt{ (w_2, w_2)} } = \sqrt{ \frac{ 3} { 2} } x \)

Identicky spočítej \( e_3 \) a máš ortonormální bázi na \( P_2 \)

Ještě koukám, že mi tam utekl člen, platí \( w_2 = v_2 - (v_2,e_1)e_1 \), ale to bylo asi jasné, protože by to nedávalo smysl odečítat vektor a skalár.