Rovnice tečny ke grafu funkce
Prosím o pomoc s příkladem:
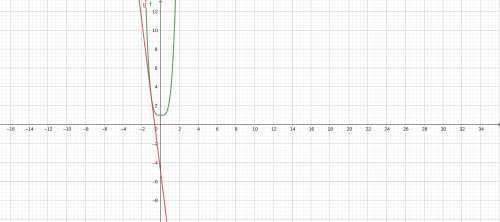
Rovnice tečny ke grafu funkce y=2x^4+1 v bodě [−1,3] je
Děkuji
Jan D.
16. 03. 2022 00:40
2 odpovědi
Zdravím,
rovnice tečny ke grafu funkce je obecně: \(y-y_0=f^\prime(x_0)(x-x_)\)
V našem případě \(f^\prime(x)=8x^3\), takže rovnice tečny je
\(y-3=8(-1)^3(x+1)\) Stačí doupravit
Jen doplním Zdeňkovu odpověď, aby ten vzorec nevypadal tak složitě tak složitě. Rovnice přímky (tedy i tečny) má obecně vzorec
\(y=kx+q\)
kde \(k\) je směrnice tečny, \(q\) vyjadřuje její posun (nebo jak to správně napsat). A v případě tečny k funkci spočítáme tuto směrnici tak, že funkci derivujeme. Jak už napsal Zdeněk, derivace zadané funkce je \(8x^3\), takže
\(k=8x^3\).
\(x\) máme zadáno, je to \(-1\), tudíž \(k=-8\).
Výpočet \(q\) je zase jen dosazovačka, protože \(y\) máme zadáno \(3\), takže
\(3 = -8\cdot (-1)+q\), tedy \(-5 = q\)
Teď známe \(k\) i \(q\) a dosadíme do výsledné rovnice:
\(y=-8x-5\)