Úprava čitatele a jmenovatele v lomeném výrazu
Ahoj,
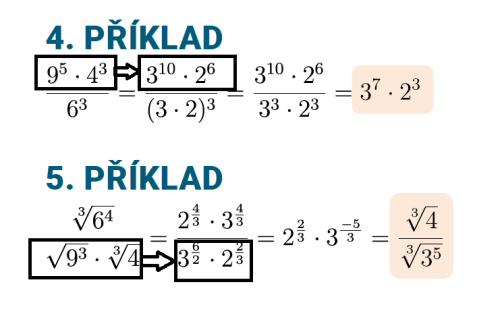
příklad ze sekce - Jak nevyletět z vejšky v prváku, Mocniny a odmocniny, příklad 4. a 5.
Jak uděláš /nějakej návod, postup, trik, případně blbého kopni/ z:
Devíti na Pátou - 3 na Desátou, Čtyř na Třetí - Dva na šestou, Druhé odmocniny Devíti na Třetí - Tři na Šest polovin a Třetí odmocniny ze 4 - Dva na Dvě Třetiny.
Mě prostě hlava nebera, jak si s tim pohraješ.
Moc děkuji, Petr
Petr K.
16. 08. 2022 15:35
3 odpovědi
Ahoj,
jde o to, jak jsou definované mocniny. Funguje to pak i na exponenty v podobě zlomků, ale pro názornost vysvětlím na celočíselných exponentech.
Když dostanu zadáno \(9^5\), tak to pro mě znamená "vypočítej \(1\cdot9\cdot9\cdot9\cdot9\cdot9\), tedy vynásob jedničku pětkrát devítkou.
Když si rozmyslím, že \(9 = 3\cdot3 = 3^2\), tak to také znamená \(1\cdot3\cdot3\cdots3\cdot3\), celkem 5 krát 2 trojky, tedy \(3^{ 10} \).
Když si takovou představu udělám pro \(3^2 \cdot 3^3\), tak dostanu, že to je \(1\cdot3\cdot3 \cdot 1\cdot3\cdot3\cdot3\), tedy jedni4ka vynásobená dvěma a třemi, tedy celkem pěti trojkami.
Funguje to i pro záporné exponenty - záporný exponent pro mě znamená dělení, tedy \(3^{ -3} = 1/3/3/3\), tedy vyděl jedničku třikrát trojkou.
Když si tohle všechno uvědomím, můžu to zformalizovat do několika vzorců:
\(a^b \cdot a^c = a^{ b+c} \)
\(\left(a^b\right)^c = a^{ b\cdot c} \)
a vlastně už zahrnutý doplněk
\(a^b / a^c = a^{ b-c} \)
Pak už zbývá jen to zapojení zlomků, které se taky dá vysvětlit celkem přímočaře... Jmenovatel ve zlomku v exponentu znamená odmocninu.
Představme si definici třetí odmocniny - \(\sqrt[3]{ a} = b \Leftrightarrow b^3 = a\)
To tedy znamená, že, když hledám, jak zapsat tu odmocninu exponentem, říká mi to \(\sqrt[3]{ a} = a^{ x} = b\) a z předchozího tedy \(b^3 = a\), tak to dle předchozího komentáře znamená, že \(b^3 = a^{ x\cdot 3} = a\), tedy \(x\cdot 3 = 1\), ergo \(x = \frac{ 1} { 3} \).
Zbytek už funguje identicky jako s celočíselnými exponenty.
Děkuji, Ta první část mi byla jasná (tady opravdu blbého nakopni). Ta druhá je horší, ale asi to taky nějak zpracuju :)