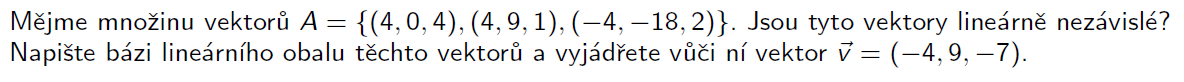Báze lineárního obalu vektorů
Dobrý den, mám skromný dotaz.
Zadání příkladu chápu, i chápu jak se dostat k řešení. Tedy vím, že je potřeba sestrojit matici, Gaussovo metodou zjistit, zdali jsou vektory nezávislé. V tomto případě jsou závislé. Potom vezmu vzniklé vektory dimenze 2 a pomocí matic zjistím jejich lineární kombinaci, která nám má dát výsledek vektoru. Jednu věc kterou nechápu je, jak zjistím, přesně které vektory jsou součástí nové báze. Pokud zjistím, že jsou závislé, které přesně mám vzít ?
Děkuji předem :-))
Petr M.
08. 01. 2023 13:17
2 odpovědi
Ahoj,
jsou dvě možnosti závislosti:
-
Jeden z vektorů je násobkem jiného. Pak prostě jeden z té dvojice vyškrtnu - je jedno který. Případně, pokud je to v zadání zbylé vektory ortogonalizuji a normalizuji. Tady asi není potřeba.
-
Jeden z vektorů vyrobím jakou součet násobků zbylých - tahle možnost je cyklická, tedy je jedno, který z vektorů vyhodím. Můžu si vybrat. Případný další postup viz bod 1)
Je to sice takové divné a nejsem si úplně jist, ale myslím, že by bází toho prostoru mohly být vektory
\(\vec{ a_1} =(1,0,1)\) a \(\vec{ a_2} =(0,-3,1)\)
nebo jakékoliv jiné, které z těch tří zadaných vypadnou, ale tyto jsou maximálně zjednodušené. Vektor \(\vec{ v} \) by měl potom v této bázi souřadnice \((-4,-3)\) (Bude mít pouze dvě souřadnice, protože už se nepohybujeme v klasickém prostoru, ale jenom v ploše, dané těmi dvěma bázovými vektory.
Pokud jsem napsal blbost, můžete mě ukamenovat :-)