Elektrotechnika
Zdravím, SOS
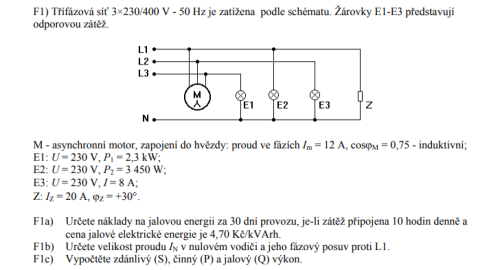
potřebuji do zítřejší půlnoci pomoct s tímto výpočtem, moc prosím.
vypočítával jsem ho už ale dnes mi učitel odepsal že to mám špatně a vůbec se teď nemůžu hnout z místa.
Petr A.
06. 05. 2021 15:47
3 odpovědi
Zapojení do hvězdy znamená, že každá fáze jde přímo na zem. Lze tedy spočítat absolutní hodnotu impedance jedné větve z napětí a proudu \(|Z| = U/I\). Do komplexních hodnot pak rozložíme jako \(Z = |Z|(\cos(75^\circ) + i\sin(75^\circ))\).
Pro žárovky - odporové zátěže spočítáme odpor dle \( P = \frac{ U^2} { R} \), resp. \(I = U/R\).
Pro zbylou zátěž obdobně větvi motoru.
Následně je potřeba posčítat paralelní impedance dle vzorce \(\frac{ 1} { Z} = \frac{ 1} { Z_1} + \frac{ 1} { Z_2} + \frac{ 1} { Z_3} + ...\). To bude slušné cvičení na práci s komplexními čísly. Jen připomínám \(\frac{ 1} { i} = -i\) a užitečný vzorec pro rozšiřování zlomků a zbavení s \(i\) ve jmenovateli \(a^2 - b^2 = (a+b)(a-b)\) a \(i^2 = -1\).
Tohle se udělá pro každou větev. Následně lze spočítat i komplexní hodnotu proudu \(I = U/R\), kde \(U = 230(\cos(50t+p) + i\sin(50t+p))\), kde \(p\) je počáteční posun fáze (0,120 a 240 stupňů).
Tyto proudy pak lze sečíst (stále komplexně) a dostane se proud nulákem.
Z proudů na jednotlivých větvích lze spočítat Příkon činný (reálný) a jalový (imaginární) dle \( P = UI\).
Následně by se mělo pro spotřebu integrovat v čase, ale vzhledem k době trvání stačí přenásobit koeficientem \(\frac{ 1} { 2} \) a vynásobit časem.
akorát koukám, že těch 50t má být 360 * 50 * t, abychom to měli ve stupních.
Počítal jsem to takto a mám to špatně ale nevím kde dělám chybu, upřímně řečeno s tím řešením navrženém od vás si nevím rady, mohl bych prosím požádat o výpočet dle vašeho řešení?