Goniometrické funkce
Dobrý den, chtěl bych poprosit o pomoc s řešením jednoho příkladu, který je možná jednoduchý, ale vůbec mně nenapadá, jak ho správně vyřešit:
"Řeka má přímý tok, šířku 150 m a rychlost proudu 1,2 m/s. Parník, jehož rychlost na klidné vodě je 3,4 m/s, míří z místa A do místa B na druhém břehu. Místo B je vzdáleno 250 m od kolmice k proudu vedené bodem A. Do kterého místa C na druhém břehumusí parník namířit, aby přistál v místě B, jestliže
a) B je ve směru proudu
b) B je proti směru proudu?
Vypočtětě vzdálenost /BC/."
Vím, jak se skládají rychlosti, vím jak se dopočítávají úhly, ale nedaří se mi nasměrovat parník tak, aby trefil místo B. Mockrát děkuji za pomoc a přeju hezký den
Vladimír J.
25. 03. 2024 13:44
6 odpovědí
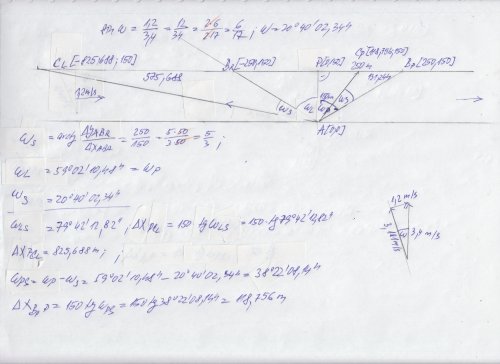
Tedy jinými slovy, místo B (na druhém břehu než bod A) je 250 m od paty kolmice k bodu A. Tedy, jestli bod B leží po proudu, tak musí cílit o nějaký úhel před B, pokud B je proti proudu, tak také musí cílit o nějaký úhel před B, tedy v obou případech musí být směrový úhel výjezdový sigma AB být o něco menší , než sigma AB cílový a sice o hodnotu delta omega, která eliminuje boční snos. S tím samým se musí počítat při letu v letadle, tak se uvažuje tzv. boční snos
V tomhle případě musíme brát jako přeponu tu rychlost parníku a kratší odvěsnu tu rychlost vody, pak se dá dopočíst rychlost parníku umenšená tou vodou a také úhel, o který proti směrovému úhlu na cílový bod namířit loď, čili fakticky výchozí azimut při dané rychlosti parníku je co vyjde viz níže.
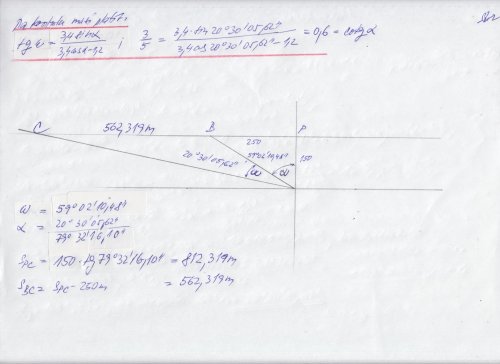
Musím říci, že ten výpočet není zcela správný, ale nicméně i když zjednodušený téměř "sedí". Správný úhel, o který musí mířit osa parníku více vlevo pro bod C vlevo bude 20°30´05.62" , zatímco z přibližného výpočtu vyšel 20°40´02.34", rozdíl cca 10 minut, výpočet níže :
Vlastně se musí sestavit rovnice, kde musí na jedné straně figorivat tg úhlu té spojnice AB a to se musí rovnat tg úhlu, vypočtenému z x-ových a y-ových složek rychlostí. Voda má jen x- ovou, a ta se odečte od x-ové složky rychl. parníku, osa x je ve směru proudu vody a osa y kolmo na řeku na druhý břeh.
Níže výpočet pro levý bod :
k tomu:
Děkuji za pomoc a přeji hezký den.