Graf lineární funkce

Ahoj,

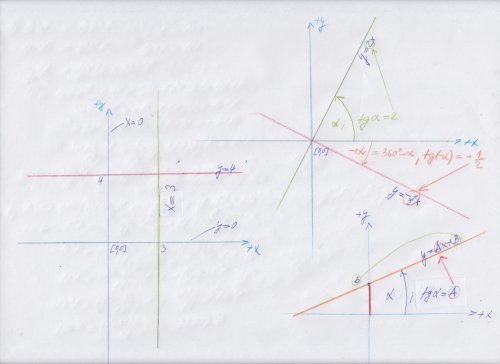
v těchto dvou příkladech \( b=0 \).

Zvol si libovolné číslo \( x \), vypočítej \( y \), dostaneš souřadnice jednoho bodu. Podobně získáš druhý bod. Graf je přímka spojující tyto dva body.

Např. zvolím \( x=0 \), dostanu \( y=2x = 2\cdot 0=0 \), mám bod \( [0, 0] \).

Graf funkce \( y=ax \) vždy prochází počátkem soustavy souřadnic. Této funkci se také říká přímá úměrnost, je to zvláštní případ lineární funkce.

Tak pro y=2x je také y=2x+0, čili prochází počátkem souřadnic, podobně y =(1/2)*x což je také y = (-1/2)x + 0, takže také prochází počátkem souřadnic, čili ta Vaše rovnice y=ax+b, tak b je úsek na ose y, čili když dosadíte do té rovnice x=0 tak dostanete právě to b a protože bylo beztak rovno nule, tak jej ani nemusíte počítat. To a je tangenta úhlu , který svírá ta přímka s osou X s kladným koncem. Takže kdyby se měla napsat například rovnice přímky, která je totožná s osou x čili na ní leží, tak to bude y=0, čili pro jakékoliv x to budou body na ose x a y k nim příslušné bude = 0, podobně, podobně rovnice přímky, rovnoběžná s osou x bude y= konstanta, čili pro jakékoliv x bude y rovno té konstantě, pokud bychom chtěli přímku rovnoběžnou s osou y, tak ta bude mít rovnici x=konstanta, prostě pro jakékoliv y bude procházet stále bodem x=konstanta na ose x a pokud bychom chtěli rovnici přímky, která leží přímo na ose y, tak to bude x=0, jelikož pro jakékoliv y bude přímka procházet stále bodem x=0 čili počátkem souřadnic viz níže :