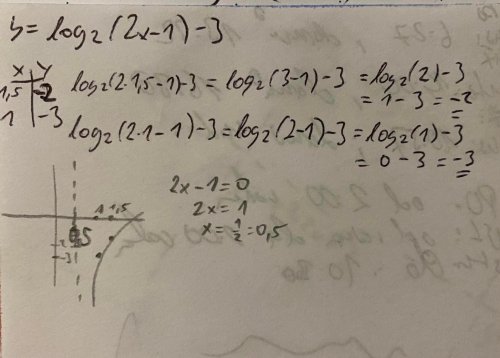Graf Logaritmu
Dobrý den, chtěla bych se zeptat jak zakreslit tento graf: \(log_{ 2} (2x-1)-3\), pokusila jsem se ho zakreslit viz. fotka.
Nicméně učitelka po nás chce, abychom za x dali 0 a tím bychom našli y. To když udělám, tak mi vyjde \(log_{ 2} (-1)\), což nejde vypočítat, že? Znamená to tedy, že to nemá řešení? Kdybych do testu použila ten jiný způsob, jakto že to vychází a zda by mi to v testu bylo uznáno?
Díky moc
Sab B.
10. 03. 2023 07:16
1 odpověď
Ahoj,
za \(x\) opravdu nulu dosadit nelze. Co lze, je vytknout v argumentu dvojku a výraz trochu přerovnat a dostaneme důležité informace:
\(\log_2(2x-1) - 3 = \log_2(2(x-\frac{ 1} { 2} ))-3 = \log_2(2) + \log_2(x-\frac{ 1} { 2} ) - 3 = \log_2(x-\frac{ 1} { 2} ) - 2\)
Vidíme tedy, že se jedná o graf logaritmu se základem 2, který posuneme o \(2\) dolů (ve směru osy y) a o \(\frac{ 1} { 2} \) doprava (ve směru osy x).
Levou asymptotu \(x = \frac{ 1} { 2} \) máš tedy dobře. Z původního průsečíku s osou \(x\), tedy bodu \([1,0]\) se stane bod \([\frac{ 3} { 2} ,-2]\). Stejně tak bod \([1,-3]) máš dobře.
Pak bych ještě spočítal průsečík s osou \(x\), tedy dosadit nulu za \(y\):
\(0 = \log_2(x-\frac{ 1} { 2} ) - 2\), tedy \(x-\frac{ 1} { 2} = 4\), tedy \(x = \frac{ 9} { 2} \)
To si myslím, že v řešení chybělo.
Otázka, jestli by něco bylo uznáno je značně subjektivní. Jde o to, jaké všechny kroky po vás vyučující chce. Obecně při sestrojování grafu funkce chceme definiční obor, obor hodnot, asymptoty, průsečíky s osami, limity v nekonečnu, 1. derivaci (minima, maxima, sedlové body, intervaly, kde roste, klesá), 2. derivaci (inflexní body, intervaly konvexnosti, konkávnosti).
Logaritmus je jednoduchý - na celém intervalu roste a je konkávní. Asymptotu máme, limita v nekonečnu je nekonečno.Definiční obor a obor hodnot sice není zapsaný, ale je z grafu zjevný. Za mě tedy chyběl pouze průsečík s osou \(x\).