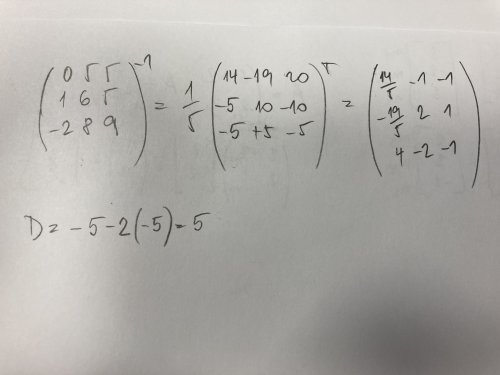Inverzní matice

Ahoj, vedle matice si zapíšeš jednotkovou matici.

Následně provádíš úpravy jako při Gaussově eliminaci (násobení řádku číslem, přičtení násobku jednoho řádku k jinému), abys dostala jednotkovou matici vlevo.

To, co vznikne vpravo bude ta inverzní matice.

Té nuly na začátku se zbavím třeba tak, že k prvnímu řádku přičtu druhý.

Děkuji za odpověď.

To, že si vedle zapíšu jednotkovou matici, mi bylo jasné. Jen ta nula...

Takže abych mohla počítat, upravím si první řádek, aby vyšlo 1 11 10 a druhý nechám 1 6 5 a třetí -2 8 9? A pak už počítám normálně?

Ještě jednou díky.

Rychlejší je u takovéto matice asi počítání pomocí determinantů. Spočítáš si determinant a pak prakticky píšeš rovnou výsledek, zkus si to najít. Jinak výsledek je

\(\left(\begin{ array} { rrr} \frac{ 14} { 5} & -1 & -1 \ -\frac{ 19} { 5} & 2 & 1 \ 4 & -2 & -1

\end{ array} \right)\)

??? Proč ten LaTeX nefunguje? Zkusím to ještě jednou jinak:

\(\begin{ pmatrix} \frac{ 14} { 5} & -1 & -1 \ -\frac{ 19} { 5} & 2 & 1 \ 4 & -2 & -1

\end{ pmatrix} \)

Nejprve byste měli vypočítat determinant matice A pomocí následujícího vzorce:

det(A) = a * ((ei) - (fh)) - b * ((di) - (fg)) + c * ((dh) - (eg))

kde a, b, c, d, e, f, g a h jsou prvky matice A, tedy pro váš případ:

det(A) = 0 * ((69) - (58)) - 5 * ((19) - (59)) + 5 * ((18) - (69))

det(A) = 0 - 5 + 5 = 0

Takže determinant matice A je nula a inverzní matice tedy neexistuje. To znamená, že matice A je singularita, tedy že nemá inverzní matici.

@Vladislave,

úvaha s determinantem sice platí, ale \(ei\) a ty další dvojpísmena ve výpočtu determinantu znamenají násobení, ne napsat čísla za sebe...

Práce tak na 5 minut

@Milan

Jak jsem psal výše, dá se to dělat snadněji, rychleji a s větší šancí neudělat chybu. Schválně jsem to znovu spočítal asi za 2 minuty, a to jsem ještě pro názornost nedělal v jednom kroku, ale ve dvou…

Tak u matice (2,2) nebo (3,3) to jde z hlavy, to není problém, ale počítat třeba takto (6,6) již znamená minory (5,5) a ikdyby tam byla jednociferná celá kladná čísla, tak "napřímo a rychle " nejdou udělat. Navíc pro technické výpočty, kde je třeba zapotřebí 10 míst a matice vysokého řádu to již není použitelné. Vy jste vlastně počítal doplňky prvků, tak pro (3,3) to jde z hlavy a pro pozici aij jste je přepisoval do pozice Aji, kde A je ten minor s příslušným znaménkem. Tak tohle při takovém zadání cca 2 minuty práce.

Však ano, netvrdím, že počítat větší matice (byť "jen" 4x4) je takto vhodnější. Reagoval jsem na to, že v době, kdy je dotaz dávno zodpovězený, tak píšete, jak je to práce na 5 minut po napsání cca 240 čísel. Tak jsem argumentoval tím, že způsob, který jsem zmínil o dva týdny dříve, je rychlejší, snadnější a bezpečnější.