Kuželosečky - hledání mnoziny bodu
Ahoj, jak se postupuje? Nevim úplně kde začít stačí mě jen trochu nasměrovat, nakreslil jsem si to, ale nevim.
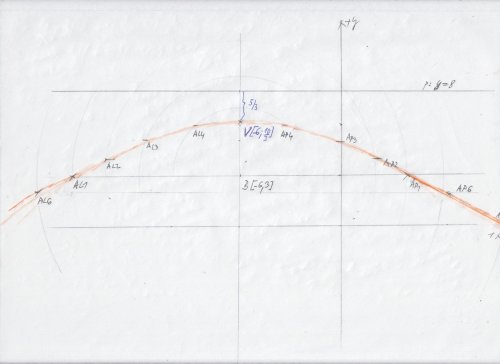
Je dána přímka p: y - 8 = 0 a bod B(-6,3) Urcete množinu bodu X, pro které platí |Xp| = 2|XB|
A K.
17. 03. 2024 10:42
4 odpovědi
Takže podrobné body získáte jako průsečík rovnoběžných přímek s tou přímkou y = 8, a oblouků kružnic o poloměru dvojnásobném, než vzdálenost těch přímek od té y = 8 .
Ten jediný, tedy vrchol : tak yB = 3 , yp = 8, delta y = 5, potom yV = yB + ( 2 / 3 ) * 5 a to je také yV = yp - ( 1 / 3 ) * 5 .
Ty ostatní prostě poloměr Ri na obě strany oblouk a rovnoběžku s y = 8 o Ri / 2 "níže" a kde se protnou, tam jsou body
U toho V mělo být yV = 3 + 10 / 3 , těch 10 / 3 je vzdálenost od bodu B
Take jsem si to tak představil avšak v řešení je zapsáno, že jde o elipsu
Elipsu ale nejde vyrobit pomocí jediného bodu a jediné přímky, a ještě splněním tohoto požadavku na stálý poměr vzdáleností, to dá jen parabolu. Právě proto, že parabola je "elipsa" které jeden vrchol utekl do nekonečna. A navíc, elipsa tím, že je uzavřená, tak bude mít prostě poloosy a to způsobuje, že se křivost mění: největší, pak nejmenší pak zase největší pak nejmenší (právě ve vrcholech poloos) a pak zase největší a tenhle požadavek jim nevyhovuje a nezařídí, aby její křivost takto plynule po pi / 2 cyklovala. To přímka nikdy nesplní, protože se skládá z nekonečně mnoha bodů a tím ty paty kolmic, od kterých se to odměřuje, utíkají na obě strany a to tu křivku "rozšiřuje" a její křivost stále klesá. Tak jestli věříte, že lze touto metodou vyrobit elipsu, pourquoi pas, quién sabé.