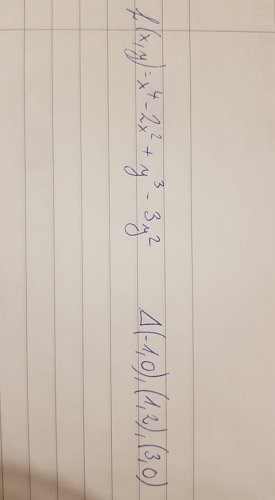Lokální extrémy a globální extrémy

Pro začátek spočítáme gradient zadané funkce:

\(Df(x,y) = [4x^3 - 4x; 3y^2-6y]\)

Nyní položíme obě rovnice rovné nule a vyřešíme pro obě proměnné.

\(x = 0, x = \pm 1; y = 0, y = 2\)

Máme tedy celkem 6 dvojic \(x,y\). Pro každou z nich si vyhodnotíme, jestli leží uvnitř zadaného trojúhelníku ( doporučuju si nakreslit, možná na to bude nějaká sofistikovaná metoda, která mě teď nenapadá.

Dále spočítáme Hessovu matici, abychom mohli tyto body klasifikovat:

\(H_{ r1} = 12x^2-4; 0\)

\(H_{ r2} = 0;6y-6\)

Omlouvám se, mělo by to být napsané jako matice, ale trochu tu bojuju s řádkováním v LaTeX bloku. Nyní spočteme determinant pro každou z dvojic s nulovým gradientem.

Pro hodnoty determinantu \(\lt 0\) máme sedlové body. Pro hodnoty determinantu \(\geq 0\) vyhodnocujeme dál, konkrétně vezmeme buď levý horní nebo pravý dolní roh (druhou derivaci podle jedné proměnné). Pokud tato je záporná, máme lokální maximum, pokud je kladná, máme lokální minimum.

Vypočteme hodnoty funkce ve všech extrémech a tu největší a nejmenší označíme za extrém globální.

Po nakreslení dojdeme k závěru, že jsou přípustné všechny kombinace s \(y = 0\) a bod \([1,2]\)

Po dopočítání Hessiánu dostaneme:

\([1,2] \rightarrow H = 8\cdot 6 = 48, min\)

\([-1,0] \rightarrow H = 8\cdot (-6) = -48, sedlo\)

\([0,0] \rightarrow H = (-4)\cdot (-6) = 24, max\)

\([1,0] \rightarrow H = 8\cdot (-6) = -48, sedlo\)

Jelikož extrém máme vždy jen jeden, lze je na zadané množině prohlásit za globální.

Zdravím, vychází mi \( f(0, 0) = 0 \) a \( f(3, 0) = 63 \), což je větší hodnota, ale můžu se mýlit.

Pravda, zapomněl jsem na důležitý krok... Pro určení extrémů je ještě potřeba vyhodnotit hodnoty na hranici oblasti - gradient tam může být nenulový, ale hodnota extrémní.

Nejsnáze asi tím, že si hranici rozdělíme na přímky

\(y = -x + 3\), \(y = x + 1\) a \(y = 0\) a vyšetříme chování funkce v závislosti na \(x\) po dosazení v jednotlivých případech.

1. \(f(x) = x^4 - 2x^2 + (3-x)^3 - 3(3-x)^2\), kde \(x \in [1,3]\)

\(f'(x) = 4x^3 - 4x - 3(3-x)^2 +6(3-x) = 4x^3 - 3x^2 + 8x - 9\)

Tato první derivace je pro \(x=1\) nulová a následně podél přímky (vyšší \(x\) ) kladná - maximum podél hranice bude na konci - v bodě \([3,0]\). Minimum pak v bodě \([1,2]\), což odpovídá již nalezenému lokálnímu minimu.

2. \(f(x) = x^4 - 2x^2 + (x+1)^3 - 3(x+1)^2\), kde \(x \in [-1,1]\)

\(f'(x) = 4x^3 - 4x + 3(x+1)^2 - 6(x+1) = 4x^3 + 3x^2 - 4x - 3\)

Nulové body této derivace jsou \(x = \pm 1\) a \(x = -\frac{ 3} { 4} \). Mezi nimi je derivace nejprv kladná a následně záporná. Minima tak nalezneme pro hodnoty \(x = \pm 1\), maximum pak pro hodnotu \(x = -\frac{ 3} { 4} \).

3. \(f(x) = x^4 - 2x^2\), kde \(x \in [-1,3]\)

\(f'(x) = 4x^3 - 4x\)

Nulové body této funkce už máme výše - \(x = \pm 1\) a \(x = 0\). Z analýzy znamének vidíme, že extrémy funkce budou po řadě: min \(x = -1\), max \(x = 0\) , min \(x = 1\), max \(x = 3\).

Na hranici tedy celkem máme extrémy:

\(f(3,0) = 63\)

\(f(1,2) = -5\)

\(f(-1,0) = -1\)

\(f(-\frac{ 3} { 4} ,\frac{ 1} { 4} ) = -\frac{ 251} { 256} \)

\(f(1,0) = -1\)

\(f(0,0) = 0\)

Globální maximum je tedy v bodě \([3,0]\), globální minimum odpovídá tomu lokálnímu \([1,2]\).

Pro ostatní body by bylo potřeba ještě vyhodnotit, jestli gradient ve směru kolmém na hranici odpovídá směru (růst/pokles), který lze očekávat pro daný typ extrému. Př. - když mám z hlediska hranice maximum, musí mi funkce v kolmém směru dovnitř oblasti klesat, abych mohl tento bod označit za lokální maximum.