Pólová vzdálenost

Pokud neuvažujeme precesi zemské osy tak musí být poloha pozorovatele o 90° jižněji (na severní polokouli toto místo nenajdeme). Takže to musí být 47° j. š. a níže k pólu.

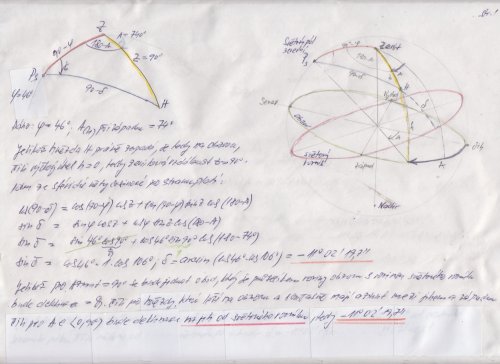
Tak ta precese ale udělá cca za 25 520 let toto: severní světový pól "zatím" je stále více severním světovým pólem, ale asi ( * ) ještě asi 90 let, od té chvíle se nezadržitelně bude světový severní pól odchylovat a sice k hvězdě Lyra v souhvězdí Vega, ale to se stane naplno za cca 13 000 let ( * ), takže času dost. Čili rychlost úhlové změny co se severního světového pólu týče je cca 23.5°/ 13000 let tedy asi 0.018" za den, ale protožeto je precesní kružnice a ne úsečka, tak ještě méně. S touhle přesností se ale úhel prostě nedá měřit, střední chyba určení zenitového úhlu je cca 0.1 " tedy asi 5* větší, takže zbytečná starost uvažovat precesi, když zenitový úhel především závisí s hlediska přesnosti určení na tížnicových odchylkách a jelikož většina hvězdáren se z praktických důvodů vyskytuje především ve vysokých nadmořských výškách kvůli refrakci a přezáření oblohy, tak ve vysokých horách zejména jsou značné tíhové anomálie řádu vteřin, které se musí zjišťovat gravimetry, což je velmi složitá záležitost, viz například SJTSK, který používá silně zastaralý Besselův elipsoid, s velkou astrogeodetickou odchylkou na trig. bodě Herrmanskogel asi 6" a "dělá" se, že to nevadí. Takže precesi, i nutaci použít můžeme a stejně to nic neovlivní Jinak ten výpočet (týká se ale něčeho trochu jiného) je podle tohoto obrázku viz níže :

A jinak, oni se neptají v té otázce nahoře, jaká musí být zeměpisná šířka pozorovatele, ale jaká musí být pólová vzdálenost, ze které nejsou vidět objekty, které jsou pozorovatelné na 43° sev. zem. šířky. Pólová vzdálenost hvězdy je strana nautického trojúhelníku ( v tom obrázku ) , čili to 90°- delta, čili doplněk deklinace do 90°. Samotná deklinace se ale nedá naměřit, protože to jsou rovníhové souřadnice 1. a 2. druhu, jedny "nezávislé" na čase, druhé ale ano. Rektascenze je pak úhel mezi deklinačními kružnicemi, tou co prochází hvězdou a tou co prochází jarním bodem, přičemž hodinový úhel jarního bodu se mění s časem a hodiový úhel jarního bodu ja fakticky hvězdný čas. Pak s ( hvězdný čas ) = alfa rektascenze + t ( hodinový úhel hvězdy ). Naměřit se ovšem dají pouze obzorníkové souřadnice, jenže zeměpisné souřadnice co se zeměpisné šířky týče, jsou zase určeny pomocí obzorníkových, takže to je o poněkud složitější.

Takže ta otázka je poněkud podivná, vlastně měla cca být, vypočtěte pólovou vzdálenost hvězdy čili její doplněk její deklinace do 90°, která (tak vypočtená hvězda) již není vidět ze stanoviska, nacházejícího se na 43° severní zem. šířky. O žádném jiném místě pozorovacím tu není řeč. Prostě co již není vidět ze 432°se. z. š. a k tomu dopočíst deklinaci a pak teprve doplněk do 90° , výpočet musí vypadat cca jako obrázek níže :

Prostě ten, kdo tu otázku pokládal, ji zapsal poněkud chybně, mělo být : vypočtěte, od jaké pólové vzdálenosti alias doplňku deklinace již nejsou vidět objekty na 43° (s.z.š.), čili znamená to určit, jaký je zenitový úhel té hvězdy ( nebo jeho doplněk výškový úhel hvězdy do 90° ) , z toho pak přepočíst deklinaci a od toho výškového úhlu, kterému odpovídá jistá deklinace, již tyto objekty nebudou na stanovisku 43° s.z.š již pozorovatelné. Prostě díváme se na ohlohu a různé hvězdy mají různou deklinaci

(a také doplněk do 90°= pólová vzdálenost) a ty hvězdy, co jsou již na obzoru a dále také pod obzorem, tak nejsou vidět a těm odpovídá jistá deklinace a tu je nutno vypočíst z nautického trojúhelníku a na to se dá přijít z toho obrázku. Jinak to ( * ) mělo být to, s čím se počítá v tabulkách efemerid, tedy polohy hvězd v různých určitých časech.

Prostě zeměpisná šířka se nedá jen tak sčítat s pólovou vzdáleností, to jsou dva zcela odlišné pojmy, jsou svázány v nautickém trojúhelníku, kde jsou prvky Z ( zenit ) PS ( světový pól ), H ( hvězda či objekt ) , mezi Z, PS je doplněk zeměpiné šířky do 90°, mezi PS H je doplněk deklinace do 90° = pólová vzdálenost, mezi Z H je zenitový úhel ( ten je také to co můžeme opravdu v terénu naměřit ) , pak při PS je hodinový úhel ( je svázán s rektascenzí ) , při Z je doplněk azimutu do 180° ( ten také můžeme v terénu měřit ) , při H je tzv. paralaktický úhel hvězdy ( není tam označený, nemá takový význam ) , PS Z a PS H je vlastně úhel mezi dvěma deklinačními kružnicemi

Takže, správná odpověď na otázku pro jakou pólovou vzdálenost nejsou ze stanoviska na 43° SZŠ vidět hvězdy je následující : hvězdy s menší úhlovou vzdáleností od světového severního pólu, než je zeměpisná šířka stanoviska, NIKDY NEZAPADAJÍ, jsou takzvané circumpolární čili zde bude jejich pólová vzdálenost menší, než 43° čili jejichž deklinace je větší než +47°. Naopak, hvězdy, jejichž pólová vzdálenost od jižního světového pólu je menší než zeměpisná šířka stanoviska na severní polokouli tedy NIKDY NEVYCHÁZEJÍ pro pozorovatele na té severní zeměpisné šířce ( a podobně to "funguje" naopak ) . Takže je vidět, že abychom je tedy nespatřili ( ty hvězdy ) ze 43° SZŠ, musí mít pólovou vzdálenost od jižního světového pólu menší než 43°, čili fakticky vůči severnímu světovému pólu se jedná o pólovou vzdálenost menší než 180°- 43°= 137°, tedy s deklinací - 47° až - 90° , tak tyto nikdy nevyjdou vzhledem ke stanovisku 43° SZŠ nad obzor ( a proto ani nemohou zapadnout, když nejprve ani nevyjdou ). Čili to také znamená, že například kdyby se jednalo o stanovsko 45° SZŠ, tak lze spatřit hvězdy s deklinací až -45° (ale ne třeba -46° až -90° ) pokud by stanovisko bylo přímo na severním pólu, pak nelze spatřit hvězdy s deklinací 0° až - 90° tedy s pólovou vzdáleností větší, než 90° ( a podobně i na jižním zeměpiném pólu ) . Pokud by bylo stanovisko přímo na rovníku na 0° (ani severní ani jižní zem. šířky), tak lze spatřit prakticky všechny hvězdy nebeské sféry, přičemž všechny budou vycházet a všechny budou zapadat. Jen přímo hvězdy s deklinací cca 90°, -90° , tedy s pólovou vzdáleností 0° ( na tu či onu stranu k severnímu světovému či jižnímu světovému pólu ) tak ty ani nevyjdou ani nezapadnou, budou přímo na obzoru čili prakticky nevidět. Deklinace k severnímu světovému pólu je kladně, k jižnímu světovému pólu záporně. Takže třeba z Isla Hierro na Kanárském souostroví na 28° SZŠ se dá spatřit větší část souhvězdí Jižního Kříže, ( deklinace cca -55° až -65°, pólová vzdálenost 25° až 35° takže část souhvězdí s pólovou vzdáleností od 28° do 35° lze z 28° SZŠ spatřit .