Pomoc před maturitou
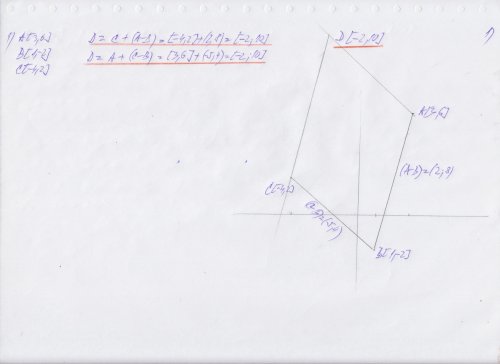
- Jsou dány body A, B, C. Určete souřadnice bodu D tak, aby čtyřúhelník A, B, C, D byl rovnoběžník.
A [3;6]
B [1;-2]
C [-4;2]
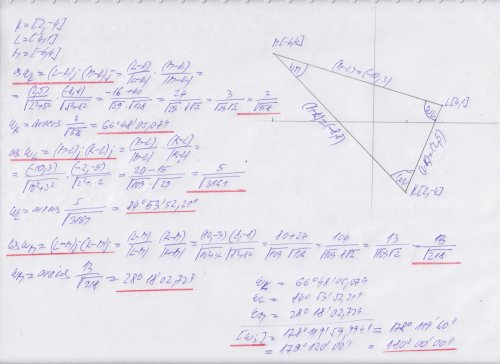
- Trojúhelník je určen vrcholovými body K, L, M. Určete všechny vnitřní úhly trojúhelníku.
K [2;-4]
L [4;-1]
M [-6;4]
- Určete rovnici přímky procházející počátkem souřadnic a svírající úhel alfa s přímkou p.
Alfa = π/3
p: y=3x-6
Lucie P.
23. 03. 2023 16:53
9 odpovědí
viz níže :
viz níže :
viz níže
Zdravím.
- příklad: přímka \(p:3x-y-6=0\) má normálový vektor \(\vec n_p=(3;-1)\)
Hledaná přímka \(q\) prochází počátkem, takže její rovnice bude \(q:kx-y=0\) a její normálový vektor \(\vec n_q=(k;-1)\)
Pro odchylku dvou vektorů platí \(\cos\alpha=\dfrac{ \vec n_p\cdot \vec n_q} { |n_p|\cdot|n_q|} \)
Po dosazení \(\dfrac12=\dfrac{ 3k+1} { \sqrt{ 10} \cdot\sqrt{ k^2+1} } \)
Po umocnění a troše úprav dostaneš kvadratickou rovnici \(13k^2+12k-3=0\), která má řešení \(k_{ 1,2} =\dfrac{ -6\pm5\sqrt3} { 13} \)
Obě řešení vyhovují.
ještě ta druhá přímka:
Moc děkuji za pomoc ️
Kdyby byla ještě nějaká jednodušší verze příkladu číslo 2 bylo by to super ️
Jen díky tomu, že ten úhel alfa je 60°, ta kvadratická rovnice vychází "jako hezky", být to ale obecný úhel, tak již ani náhodou, musil by se tam vyčíslovat cos ^ 2 alfa pro dva členy, které by figurovaly v tom diskriminantu, abychom z "toho" dostali směrník té přímky. Takže praktičtěji asi jinak.
Tak k příkladu 2, chtěli po Vás, abyste uměli vypočíst úhel mezi dvěma úsečkami, které mají zadané koncové body v souřadnicích, a to je vždy jako arccos ( skalární součin dvou jednotkových vektorů vložených do těch úseček) ) (v jakémkoliv prostoru) . Takže jednodušeji by to také šlo, musily by se vypočíst spojnice (délky) pak třeba jako cosinovou větou, ale není to příliš praktické viz níže :
