Racionální funkce
Dobrý den,
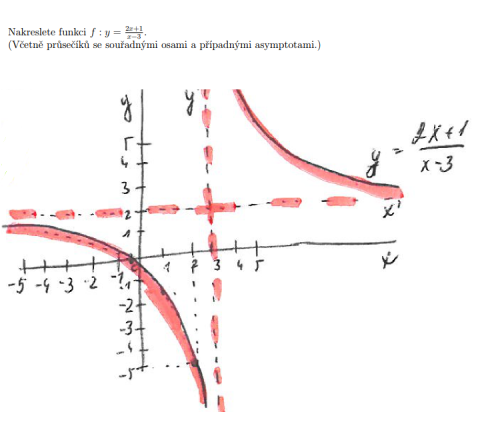
- Nakreslete funkci f : y = 2x+1/
x−3.
(Včetně průsečíků se souřadnými osami a případnými asymptotami.) Viz obrázek.
Potýkám se problémem jak určit horizontální asymptotu.
Vertikální co jsem pochopil tak se určuje podle jmenovatele, kde se hledá hodnoty = 0, tedy když mám x-3 tak hodnota vertikálního je 3.
Horizontalní se počítá tak že si v jak ve jmenovateli a čitateli vyhledám kde a co obsahuje x? V tomto případe 2x/x dosádím například 1 a vyjde mi hodnota 2?
Dále si do celé funkce dosádím hodnotu abych zjistil body a pomocí nich nakreslím ty dolní a horní asymptoty?
Děkuji za případnou radu
Jouda M.
19. 01. 2024 21:39
8 odpovědí
Takže jestli to chápu správně, tak ten vertikální se počítá tak jak jsem zmiňoval a ten horizontální podle limity? Jak se zde vypočítal?
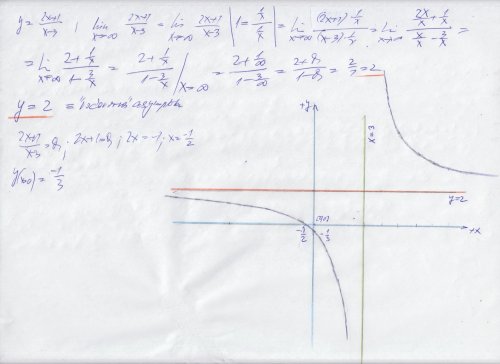
Ano, svislá asymptota je v tomto případě dána výrazem ve jmenovateli, ze kterého vzejde rovnice přímky x = 3 , jelikož se nemůže rovnat nule, tedy v x = 3 je svislá přímka alias asymptota, se kterou se ten graf "nesetká" . V jiných případech ale může svislá asymptota být dána i poněkud jinak, např. pro y = x * e ^ ( 1 / x ) má svislou asymptotu v x = 0 proto, že je tam v exponentu výraz 1 / x a z něj plyne ta svislá asymptota v x = 0 . vodorovná vyplyne z limity a obecně může být také šikmá asymptota, která je dána přímkou o rovnici y = k * x + q a pak se opět z limity , když x jde k nekonečnu pro poměr f ( x ) / x určí směrnice "k" té asymptotické přímky a úsek "q" se určí jako limita , když x jde k nekonečnu rozdílu ( f ( x ) ) - k * x ) a ta vodorovná je jen zvláštní případ šikmé, protože víme, že k = 0 ( je rovnoběžná s osou x ) a úsek na ose y je vlastně přímo ta rovnice přímky alias asymptoty , zde y = 2 ( u šikmé by to bylo to "q" ).
Ještě poslední otázky je na ty body -1/2 s -1/3. Nějak mi není podle obrázku jasné jak jste je vypočítal. To jste také dělal podle limity?
Ne, jen pouhým výpočtem, pro y = ( 2 * x + 1 ) / ( x - 3 ) , když se dosadí za x = 0 , dostaneme y = ( 2 * 0 + 1 ) / ( 0 - 3 ) = 1 / - 3 = - 1 / 3 , prostě y ( x = 0 ) = - 1 / 3 , to proto, že x = 0 je rovnice osy y a pak nám tedy vyjde průsečík křivky s osou y. Obráceně, abychom dostali, kde graf protíná osu x, tak se položí y = 0, tedy ( 2 * x + 1 ) / ( x - 3 ) = 0 , to je po úpravě 2 * x + 1 = 0 , 2 * x = - 1 , x = - 1 / 2 , to proto, že y = 0 je zároveň rovnice osy x (a tím y - em je přímo ten výraz ( 2 * x + 1 ) / ( x - 3 ) . Obecně ale vypočíst průsečíky s osou x je velmi složité, ikdyž je funkce zadána explicitně ve tvaru y = f ( x ) jako zde, vede to v řadě případů na rovnice vyššího stupně a jejich kořeny (to jsou ty průsečíky) nejdou vyjádřit konečným počtem algebraických úkonů, resp. když bude ta rovnice křivky zadána implicitně, ve tvaru z = f ( x , y ) , tedy z = 0 , tedy f ( x , y ) = 0 tak nepůjde nijak vyjádřit buď x = g ( y ) , nebo y = h ( x ) , aby se výše uvedeným způsobem určily průsečíky s osami, tj. položit ve výrazech h ( x ) pro ( x = 0 ) nebo g ( y ) pro ( y = 0 ) . Tady to je velmi jednoduché .
Děkuji moc za pomoc při pochopení.
Zdravím.
Jen doplnění dalšího možného postupu.
\(\frac{ 2x+1} { x-3} =\frac{ 2x-6+7} { x-3} =\frac{ 2(x-3)} { x-3} +\frac7{ x-3} =2+\frac7{ x-3} \) a okamžitě vidíš asymptoty, protože fce
\(y=m+\frac{ k} { x-n} \) má svislou asymptotu \(x=n\) a vodorovnou \(y=m\) (pro \(k\ne0\))