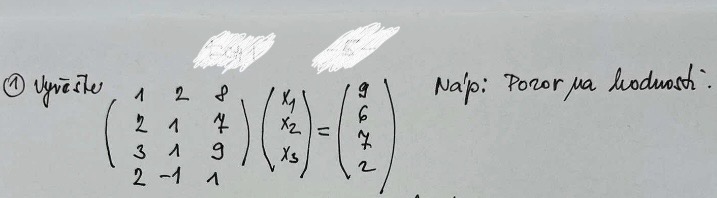
Řešení matice (jakou metodou?)

Můžete si to přepsat do jedné matice s pravou stranou. Ale vyjde Vám, že tři řádky té matice A jsou lineárně závislé, ale pravá strana, která k nim přísluší, tak ve dvou případech jsou ty řádky včetně pravé strany nastejno, čili jeden vyškrtnout, a zbyde druhý a třetí, přičemž druhý bude mít vzhledem ke třetímu odlišnou pravou stranu. To fakticky znamená, že se jedná o dvě přímky y + 3z = 4 a y + 3z = 16/5 a ty jsou rovnoběžné, čili se neprotnou a nemohou mít spolu průsečík. Kdyby nebylo té třetí rovnice (nebo té druhé rovnice) , tak bude řešením přímka a všechny body na ní, kdyby zbyla jen jediná rovnice, tak by řešení leželo v rovině a všechny body na ní. Zde ale je rozpor, první s druhou dá řešení v rámci nějaké přímky a první s třetí v rámci jiné přímky, ale druhá s třetí nikoliv, prostě nejsou takové body o souřadnicích x1,x2,x3, aby vyhověly všem třem rovnicím, tak je to vidět z toho, když odečtete třetí rovnici od druhé, vyjde Vám 0 x + 0 y + 0 z = 16/5 - 4 = - 0.8, což nelze.

Metodou nejmenšího součtu čtverců oprav by to za určitých okolností také šlo, ale zde ne, protože sloupce matice A (po transpozici řádky) jsou lineárně také závislé. Totiž jeden "nějaký" sloupec je lineární kombinací "ostatních dvou", kdyby nebyl, tak ano, ale protože je, tak i matice ATA nebude mít lineárně nezávislé řádky a nepůjde invertovat. Ve vyrovnávacím počtu by se tomu řeklo, že je tzv. "špatně" podmíněná, ta matice A. A jedná se ne o nejmenší čtverce jednotlivých oprav, ale nejmenší součet druhých mocnin oprav, tedy čtverců oprav. Takže třeba aritmetický průměr nebo obecný vážený průměr je vlastně také výsledkem MNČ (aritmetický má matici vah = jednotkové) viz níže: