Slovné úlohy
1.Dĺžky strán a dĺžka uhlopriečky obdĺžnika sú tri po sebe idúce členy
aritmetickej postupnosti. Dĺžka dlhšej strany obdĺžnika je 12 cm . Určte v centimetroch
štvorcových obsah tohto obdĺžnika.
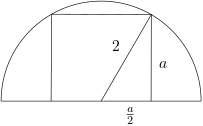
2.Do polkruhu s polomerom 2 cm je vpísaný štvorec. Vypočítajte v centimetroch štvorcových obsah tohto štvorca.
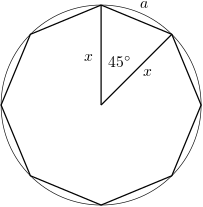
3.Vypočítajte v decimetroch obvod pravidelného osemuholníka, ktorý má obsah 16 decimetrov štvorcových.
Julia B.
22. 11. 2020 14:09
4 odpovědi
Zdravím
- jestliže delší strany je 12, pak kratší strana je 12-d a úhlopříčka je 12+d
Z Pythagorovy věty máš \((12-d)^2+12^2=(12+d)^2\)
a dopočítáš d, pak kratší stranu a platí \(S=ab\)
- Na obrázku vidíš pravoúhlý trojúhelník. Pythagorova věta
\(4=a^2+\left(\frac a2\right)^2\)
Vypočítáš \(S=a^2\) a je to
- Na obrázku vidíš trojúhelník. Jeho obsah je \(S=\frac12 x^2\sin45^=\frac{ \sqrt2} 4x^2\circ\)
V osmiúhelníku je takových trojúhelníků 8, takže podle zadání platí
\(16=8\frac{ \sqrt2} 4x^2\circ\ \Rightarrow\ x^2=4\sqrt2\) (dm^2)
Stranu a vypočítáš z kosínové věty \(a^2=x^2+x^2-2x^2\cos45^\circ\)
Obvod pak je \(o=8a\)
Kuknite toto video, super vysvetlené! :)