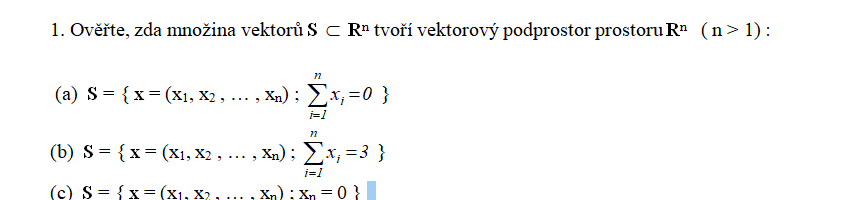Vektorový podprostor

Pro zjištění, jestli je množina vektorový prostor, musíš ověřit, že platí všechny axiomy týkající se tělesa, a že množina splňuje definici vektorového prostoru.

Protože \( \mathbb{ R} ^n \) je vektorový prostor, nemusíš ověřovat axiomy týkající se tělesa, stačí zjistit, jestli (a) \( S \) obsahuje nulový vektor, (b) \( S \) je uzavřená na sčítání vektorů, (c) \( S \) je uzavřená na násobení vektoru skalárem

(a) \( 0 = (0, ...0) \) a \( \sum^n 0 = 0 \) takže \( 0 \in S \)

(b) pro \( u, v \in S \) platí \( \sum^n u_i + v_i = \sum^n u_i + \sum^n v_i = 0 + 0 \) takže \( u + v \in S \)

(c) pro \( u \in S \) platí \( \sum^n \lambda u_i = \lambda \sum^n u_i = \lambda 0 = 0 \) takže \( \lambda u \in S \)