Vennovy diagramy - slovní úloha procenta

Zdravím,

tady Vennovy diagramy nepotřebuješ. Co se týče procent, řekni si, že ve třídě je 100 lidí a každý člověk ti bude dělat jedno procento.

Pak podle zadání bude 70 chlapců a 30 dívek, 75 lidí bude chodit na francouzštinu a 75 na latinu.

A nyní začni kontrolovat jednotlivá tvrzení:

a) To je pravda. I kdyby všechny dívky chodily na latinu, pořád 35 lidí chybí a to musí být kluci.

b) To je taky pravda. Čtvrtina ze 70 je 18 (zaokrouhleno na celá čísla) a chybí v latině i fránině 57 lidí a ty dívkami nedoplníš, takže kluků musí bý více.

c) To je opět pravda. I kdyby všichni kluci chodili na fr. pořád jich není dost a musí je dívky doplnit do 75.

d) Tohle neplatí. Klidně můžeme mít 51 studentů na latině i fr. Oba předměty doplníme 24 lidmi a zbyde nám jeden, který nechodí ani na jeden z uvedených jazyků.

e) Tohle je správně. Kdyby 26 lidí nestudovalo ani jeden z uvedených jazyků, pak nám nezbývá dost lidí na doplnění do 75 na jednotlivé jazyky.

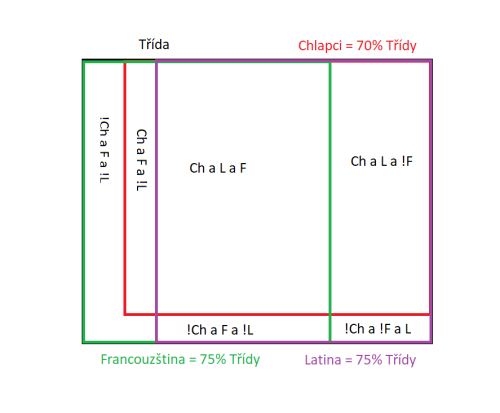
V příloze diagram...

Jinak k vyhodnocení těch možností: Budeme předpokládat, že máme 100 studentů, ať můžeme počítat s čísly. Navíc předpokládejme, že "Kdo není chlapec, je dívka".

Máme tedy 70 chlapců a 30 dívek, 75 studentů Francouzštiny a 75 studentů Latiny.

a) Mezi studenty, kteří chodí do latiny, je vice chlapců než dívek?

Budeme uvažovat nejhorší možný scénář - co nejvíce dívek na Latině, tedy všech 30. Zbývá nám ještě 45 míst pro chlapce, takže ANO, je jich tam víc.

b) Alespoň čtvrtina chlapců chodí do francouzštiny i do latiny?

V nejhorším případě obsadíme v obou jazycích co nejvíce míst děvčaty. Tedy zbyde mi 45 míst v každém (viz a) pro chlapce. Chlapců mám 70, v nejhorším případě tedy potřebuju, aby jich 20 (\(2\cdot 45 - 70\)) chodilo na oba jazyky. \(\frac{ 20} { 70} = \frac{ 2} { 7} > \frac{ 2} { 8} = \frac{ 1} { 4} \). Tedy ANO.

c) Do francouzštiny chodí alespoň jedna dívka?

Máme 75 míst a jen 70 chlapců. Chodí tam tedy alespoň 5 dívek, tedy ANO.

d) Právě polovina studentů chodí do francouzštiny i do latiny?

Francouzština a Latina mají dohromady 150 míst. V nejhorším případě je potřebuju obsadit všemi (100) studenty, tedy alespoň 50 bude muset chodit na obojí. V nejhorším případě je tedy polovina splněna. Je ale možné, že se jazyky překryjí více - pokud existuje student, který nechodí ani na jeden z předmětů. Tedy NE.

e) Nejvýše pro 25 procent studentů platí, že nechodí ani do latiny, ani do francouzštiny.

Nejhorší případ v tuhle chvíli je, že se překrejí studenti, co chodí na Latinu i Francouzštinu - tedy obsadím tato místa jen 75 studenty. V nejhorším případě nechodí nikam 25, tedy i 25% studentů. Tedy ANO.

Koukám, že ten diagram není dobře - chybí mi tam kombinace NOT F a NOT L pro obě pohlaví.