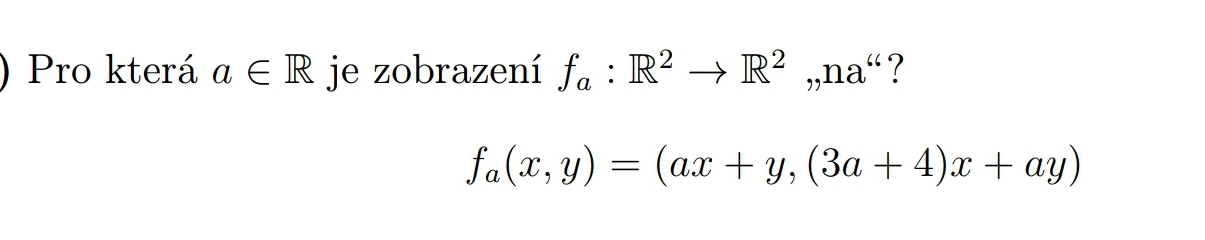Zobrazení s parametrem

V obecném případě vyjdeš z definice. Zobrazení je na, pokud pro každé \( (u, v) \in R^2 \) existuje \( (x, y) \in R^2 \), aby platilo \( f_a(x, y) = (u, v) \). Tenhle vztah dává soustavu rovnic

\( ax+y=u \\ (3a+4)x+ay=v \)

Když ji vyřešíš pro \( x \), dostaneš \( x=\frac{ au-v} { a^2-3a-4} \). Ze zlomku už vidíš hodnotu parametru \( a \), pro který nebude existovat řešení a \( f_a \) nebude na. Stejný výpočet uděláš i pro \( y \).

Existuje i jednodušší postup, ale to záleží na tom, v jakém pořadí si vysvětlujete látku. Zobrazení je na právě tehdy, když je prosté, takže stačí řešit homogenní soustavu rovnic

\( ax+y=0 \\ (3a+4)x+ay=0 \)

Vyjádříš si \( y \) z první rovnice a dosadíš do druhé, abys zase dostala kvadratickou rovnici. Když je \( a \) řešením rovnice, tak bude existovat netriviální řešení pro \( (x,y) \) a pak funkce není prostá ani na.