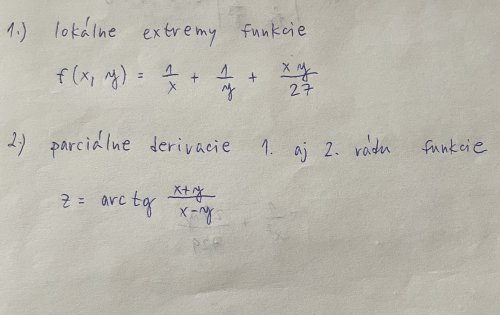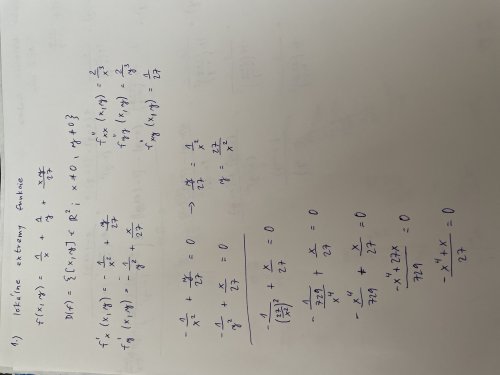Extremy,derivacie

Úloha 1

První derivace:

$\displaystyle \frac{ \partial f} { \partial x} =-\frac{ 1} { x^2} +\frac{ y} { 27} =0$

$\displaystyle \frac{ \partial f} { \partial y} =-\frac{ 1} { y^2} +\frac{ x} { 27} =0$

Soustava rovnic má řešení (3, 3), což je stacionární bod.

Druhé derivace:

$\displaystyle \frac{ \partial^2 f} { \partial x^2} =\frac{ 2} { x^3}$

$\displaystyle \frac{ \partial^2 f} { \partial y^2} =\frac{ 2} { y^3}$

$\displaystyle \frac{ \partial^2 f} { \partial x \partial y} =\frac{ 1} { 27}$

V bodě (3, 3) je (po dosazení) následující hodnota kladná

$\displaystyle D=\frac{ \partial^2 f} { \partial x^2} \cdot \frac{ \partial^2 f} { \partial y^2} -\left[\frac{ \partial^2 f} { \partial x \partial y} \right]^2>0$

je zde tedy ostrý lokální extrém, a protože

$\displaystyle \frac{ \partial^2 f} { \partial x \partial y} =\frac{ 1} { 27} >0$

je tak kladné, je zde ostré lokální minimum. Jeho hodnotu získáme dosazením (3, 3) do funkce f(x, y).

Vedeli by ste mi prosim povedat kde som spravila chybu?

Úloha 2

V tabulkách je

$\displaystyle ({ \rm arctg} (x))'=\frac{ 1} { 1+x^2}$

Funkce $z$ je složená, postupujeme tedy tak, že derivaci vnější funkce vynásobíme derivací vnitřní funkce $\frac{ x+y} { x-y}$, kterou derivujeme jako podíl, dohromady

$\displaystyle \frac{ \partial z} { \partial x} =\frac{ 1} { 1+\left(\frac{ x+y} { x-y} \right)^2} \cdot \frac{ 1\cdot(x-y)-1\cdot(x+y)} { (x-y)^2}$

po úpravách dostaneme

$\displaystyle \frac{ \partial z} { \partial x} =-\frac{ y} { x^2+y^2}$

Parciální derivace podle proměnné $y$ se počítá podobně, mělo by vyjít

$\displaystyle \frac{ \partial z} { \partial y} =\frac{ x} { x^2+y^2}$

Druhé derivace jsou derivace podílu, to už půjde? Např.

$\displaystyle \frac{ \partial^2 z} { \partial x^2} =\frac{ 2xy} { (x^2+y^2)^2}$

Úloha 1

Rovnici je nakonec potřeba upravit na součinový tvar. Ve 3. řádku zdola bych vytknul před závorku $\frac{ x} { 27}$. Už to půjde?

Ano rozumiem, mozem sa este opytat ako dostanem pri derivacii arctg podla x

$\frac{ y} { { x} ^{ 2} +{ y} ^{ 2} }$

pretoze nejak mi to nevychadza

Dakujem

Úloha 2

první řádek je jasný?

$\displaystyle \frac{ \partial z} { \partial x} =\frac{ 1} { 1+\left(\frac{ x+y} { x-y} \right)^2} \cdot \frac{ 1\cdot (x-y)-1\cdot (x+y) } { (x-y)^2} =$

$\displaystyle =\frac{ 1} { 1+\left(\frac{ x+y} { x-y} \right)^2} \cdot \frac{ -2y} { (x-y)^2} = \frac{ 1} { \frac{ (x-y)^2+(x+y)^2} { (x-y)^2} } \cdot \frac{ -2y} { (x-y)^2} = -\frac{ 2y} { 2x^2+2y^2} =\dots$

Ano rozumiem