Jak vypočítám optimální velikost hranolu?
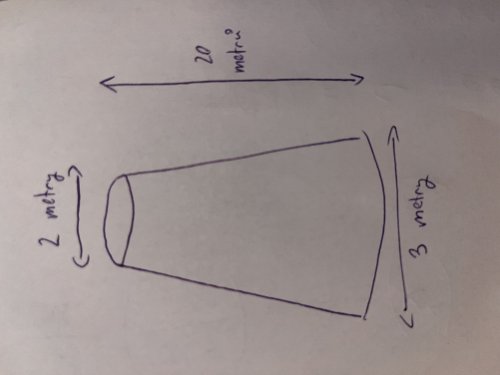
Dobrý večer. Potřeboval bych poradit s výpočtem optimální velikosti hranolu z kmene stromu o rozměrech na obrázku. Nevím si rady s tvorbou příslušné rovnice pro derivaci. Děkuji moc
Ondrej A.
05. 06. 2023 21:55
5 odpovědí
Tak především je nutné dodat, jak má ten hranol vypadat, jestli má mít stále stejný průřez v jakékoliv výšce, nebo zda to má být vlastně komolý protáhlý jehlan, dole větší průřez, nahoře menší. Pokud to první, tak výška nehraje roli, jen ten horní menší kruh je rozhodující a do něj je optimální jen čtverec. Prostě čtverec, vykrojený z kruhu má minimální odpad, který bude činit pi-2 v horním profilu. V dolním to bude (9/4)*pi-2
A ještě také, zda ten hranol má být pravoúhlý čtyřúhelník. Hranol pro stavební účely obecně nemusí mít nutně jen profil čtverce či obdélníku, ale i jiný, pak to také není levná záležitost.Takže to chce psát přesně, co je požadováno.
Ano, hranol by měl mít stále ten samý průřez a profil čtverce.
Tady máte zdůvodnění, proč čtverec je v kruhu tím optimálním pravoúhlým obrazcem i s hledáním extrému :
Ta proměnná K, podle které se derivovalo, vyjadřuje poměrnou část z poloměru coby konstanty daného kruhu (tedy jeho daného poloměru) a protože vychází čtverec, tak je to pochopitelně odmocnina ze dvou , čili ( strana a čtverce ) ku ( poloměru R ) = ( odmocnina ze 2 * R ) / R = odmocnina ze dvou.