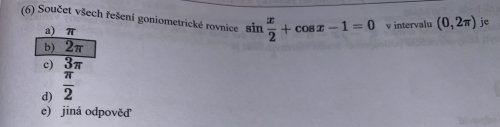Goniometrické rovnice

• cos x, samozřejmě, chyba z nepozornosti

Zkuste x = 2 * x / 2 a raději to zkontrolujte.

Výsledek, podle zadáni, resp. součet všech výsledků by měl být 2π v intervalu (0,2π). Každopádně zkusím za X = 2*X/2. Děkuji vám!

Ty triviální kořeny, kdy se x=0 nebo 2Pi nechtěli (je tam interval v kulatých závorkách, takže je zajímá jen výsledek té závorky, čili první kořen je x=pi/3 a druhý je 5pi/3, to je dohromady 6pi/3 = 2 * pi.

Oba kořeny po dosazení pasují sin (pi/3)/2 + cos pi/3 = 1, podobně sin (5pi/3)/2 + cos 5pi/3 = 1

Je možnost vypočítat toto bez kalkulačky? K arcsin to podle Vaší úvahy šlo, porozuměl, každopádně netuším jak vypočítat arcsin 1/2 z hlavy, případně za pomocí jednotkové kružnice. Pokud to je něco triviálního, tak se omlouvám, ale GON. rovnice nejsou moji silnou stránkou.

Opravdu je, je to jen záležitost nacvičit si to.Pro některé úhly to jde snadno, stačí si udělat kružítkem rovnostranný trojúhelník a jednu stranu přepůlit a máte evidentě vyrobeny úhla 30°, 60°, 90° a strana toho trojúhelníku byly jednotková, čili přepůlit dá jednu plovinu pro ten sin 30. 45° prostě nakreslíte na sebe kolmé jednotkové délky a přepona bude odm(2). Tím máte ihned sin 45°. Pokud chcete graficky sin 15°, stačí nakreslit čtverec a do něj symetricky rovnostranný trojúhelník a máte úhly 90°= 15°+ 60 °+ 15° a tím máte i automaticky grafické vztahy pro něj. Pak sin 15° bude ( odm (6) - odm (2) ) / 4, kalkulačky pro takovéto úhly netřeba. Pak třeba lze graficky odvodit 36°( v pětiúhelníku), pak 180° / 17 , pak 180 °/ 257 a nejvýš 180°/ 65537 také případně 180°/ (3 * 5 * 17 * 257 * 65537) (každé toto číslo nejvýše jen jednou) také lze neomezeně půlit. Tím jsou veškeré graficky sestrojitelné úhly vyčerpány, další, ale není na to ještě důkaz, zřejmě nejsou graficky sestrojitelné (ani algebraicky vyjádřitelné).