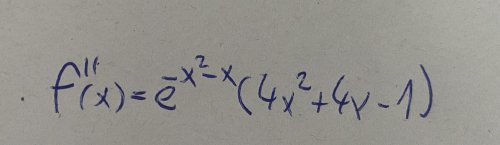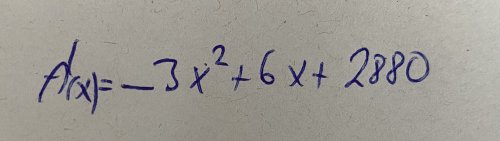Konkávni, konvenční

Zdravím.

Platí, že fce je konvexní, když \(f^{ \prime\prime} \ge0\), tj.

\(e^x(-x^2-2x+4)\ge0\). Protože \(e^x\) je vždy kladné, zůstane ti \(-x^2-2x+4\ge0\).

Po několika triviálních úpravách:

\(x^2+2x-4\le0\)

\(x^2+2x+1\le5\)

\((x+1)^2\le5\)

dostaneš

\(-1-\sqrt5\le x\le -1+\sqrt5\)

Na zbylých dvou intervalech je konkávní.

Děkuju mockrát

Pro upřesnění , pokud by y´´ byla rovna nule ( pro křivku ), tak nemůže být křivka ani konkávní ani konvexní, je to v bodě, kde je inflex ( inflexilis = neohebný, míněno nezakřivený), ve kterém přechází z konvexní na konkávní nebo z konkávní na konvexní, především proto, že y´´ reprezentuje křivost (obecně ( 1k ) = velikost vektoru (x ´´), když parametrem je oblouk, a tedy zde , když je dána vztahem y = y(x), pak ( 1k ) ^ 2 = ( y´´ ^ 2 ) / ( ( 1+( y´ ) ^ 2 ) ^ 3 ) a ta, jak z výrazu vidět, bude rovna nule, když y ´´ = 0. Prostě v okamžiku, kdy křivka dospěje do místa, kde y´´ = 0 tak má v tom bodě nekonečný poloměr křivosti (ale jen pro ten jediný bod - inflex), o cokoliv "vedle" na tu či onu stranu pak nenulovou křivost a pak tedy konvexní či konkávní podle znaménka y´´.

Děkuju moc

Mám ještě problém s tímto, nevím zda mám vytknout čtyřku či jak si s tím poradit. Děkuju moc, přidávám také už v druhé derivaci

Zdravím, je to úplně stejné.

Exponenciela je pořád kladná, tudíž tě nezajímá. Pro konvexnost zůstane

\(4x^2+4x-1\ge0\)

A opět pár triviálních úprav:

\(4x^2+4x+1-2\ge0\)

\((2x+1)^2-2\ge0\)

\((2x+1-\sqrt2)(2x+1+\sqrt2)\ge0\ \Rightarrow\ x\in(-\infty;\frac{ -1-\sqrt2} 2]\cup[\frac{ \sqrt2-1} 2;\infty)\)

OT: vypadá to, že nemáš problémy derivacemi, ale s řešením kvadratických nerovnic. Třeba by pomohlo něco si o tom vyhledat.

Opravdu děkuju moc..

Máte pravdu, budu muset se to doučit.

Omlouvám se, ale zase si neumím poradit s jedním příkladem, kde mám najít stacionární body. Nevím jak to upravit.. na internetu jsem nenašla žádný podobný. Nevěděl by sis tím rady? Děkuju..

Zdravín,

pro stacionární body platí \(f^\prime(x)=0\), takže

\(-3x^2+6x+2880=0\) - nejdřív zkrátíš -3

\(x^2-2x-960=0\) a nyní buďto přes diskriminant, nebo doplněním na čtverec (velmi pochybuju, že na internetu není nic o řešení kvadratických rovnic).

\(x^2-2x+1-961=0\)

\((x-1)^2=31^2\)

\(x-1=\pm31\), dopočítat

Zdravím všechny a jen doplním, že nulová druhá derivace neznamená inflexní bod ve smyslu bodu, "ve kterém přechází z konvexní na konkávní nebo z konkávní na konvexní". Klasický protipříklad je y(x) = x^4 v 0.

Jistěže obecně ne, ale v konkrétním případě ano.