Obvody a obsahy
Dobrý den
Pomůžete mi prosím s těmito úlohami?
Přeji hezký den
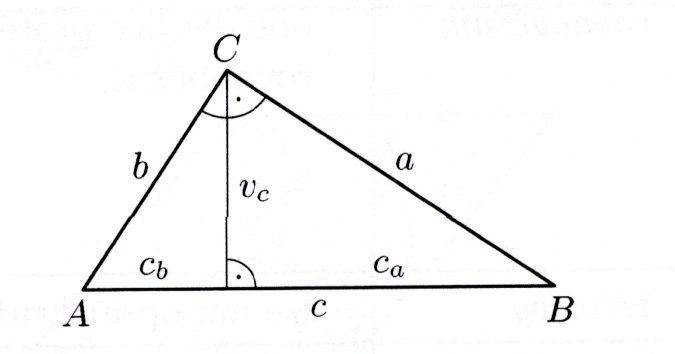
V pravoúhlém trojúhelníku ABC s pravým úhlem při vrcholu C je dáno:.b=5 cm, cb= 4cm Vypočítejte zbývající prvky (a,b,c,ca,cb,v,alfa, beta).
Strana pravidelného pětiúhelníku a=20cm.Vypočítejte jeho obsah a poloměr kružnice opsané.
Lenka K.
13. 05. 2021 17:27
9 odpovědí
K první úloze... bude zapotřebí použít: Vietovy vzorce, Pythagorovu větu a Funkci sinus. Dostaneme:
\(c * c_b = b^2 \Rightarrow c = \frac{ 25} { 4} \\
c^2 = a^2 + b^2 \Rightarrow a = \sqrt{ \frac{ 625} { 16} - 25} = \sqrt{ \frac{ 225} { 16} } = \frac{ 15} { 4} \\
c * c_a = a^2 \Rightarrow c_a = \frac{ \frac{ 225} { 16} } { \frac{ 25} { 4} } = \frac{ 9} { 4}
\)
Pro ověření - \(c = c_a + c_b = \frac{ 9} { 4} + \frac{ 16} { 4} = \frac{ 25} { 4} \)
\(\sin\alpha = \frac{ a} { c} \Rightarrow \alpha = \arcsin\frac{ 15} { 25} \approx 36.87^\circ \\
\sin\beta = \frac{ b} { c} \Rightarrow \beta = \arcsin\frac{ 20} { 25} \approx 53.13^\circ
\)
Opět můžeme pro kontrolu: \(\alpha + \beta = 36.87^\circ + 53.13^\circ = 90^\circ\)
Oprava formátu:
\(\sin\alpha = \frac{ a} { c} \Rightarrow \alpha = \arcsin\frac{ 15} { 25} \approx 36.87^\circ \\
\sin\beta = \frac{ b} { c} \Rightarrow \beta = \arcsin\frac{ 20} { 25} \approx 53.13^\circ\)
A ke druhé úloze:
Víme, že vnitřní úhel pravidelného pětiúhelníku je \(540^\circ / 5 = 108^\circ\).
Z toho můžeme dopočítat parametry trojúhelníků, které ho tvoří:
\(\frac{ v_a} { a/2} = \tan 54^\circ \\
\frac{ a/2} { r} = \cos 54^\circ \)
Tedy \(v_a = 13.76\text{ cm, a } r = 17.01\text{ cm} \). Pak už snadno \( S = 5\cdot\frac{ a\cdot v_a} { 2} = 5\cdot\frac{ 13.76\cdot20} { 2} = 688\text{ cm} ^2\)
Jak už označení napovídá, \(r\) je ten žádaný poloměr kružnice opsané.
Tak já nevím, nějak mi to formátování nejde... tak ještě jednou ty divné pasáže:
\(\sin\alpha = \frac{ a} { c} \Rightarrow \alpha = \arcsin\frac{ 15} { 25} \approx 36.87^\circ \\
\sin\beta = \frac{ b} { c} \Rightarrow \beta = \arcsin\frac{ 20} { 25} \approx 53.13^\circ\)
a
\(\frac{ v_a} { a/2} = \tan 54^\circ \\
\frac{ a/2} { r} = \cos 54^\circ \)
\(\sin\alpha = \frac{ a} { c} \Rightarrow \alpha = \arcsin\frac{ 15} { 25} \approx 36.87^\circ \)
\(\sin\beta = \frac{ b} { c} \Rightarrow \beta = \arcsin\frac{ 20} { 25} \approx 53.13^\circ\)
a
\(\frac{ v_a} { a/2} = \tan 54^\circ \)
\(\frac{ a/2} { r} = \cos 54^\circ \)
Jan P. pro Jana Z.: Před vložením příspěvku se dá ukázat "Náhled" (tlačítko je hned nad oknem pro vkládání textu) - trvalo mi asi dva měsíce, než jsem si toho všiml :) Jinak, při vkládání vzorců si nejdřív zkopíruju krajní "lomítka se závorkami" (červeně nad oknem).
Pro Lenku: Postup vložím za chvíli.
Známe stranu \( b \) a úsek \( c_b \).
Podle Pythagorovy věty vypočítáme výšku k přeponě \( v_c \) (viz obrázek), platí \( b^2=c^2_b+ v^2_c\).
Z Euklidovy věty o výšce \( v^2_c=c_a\cdot c_b \) vypočítáme úsek \( c_a \). Přepona měří \( c=c_a+c_b \).
Z Euklidovy věty o odvěsně \( a^2=c\cdot c_a \) najdeme \( a \). Úhly pomocí goniometrických funkcí. Stačí takto?
To je právě to... v náhledu to vypadalo pokaždé v pořádku. A potom ve výsledku to v pořádku být přestalo. Ale asi to dělá to odřádkování v rámci jednoho LaTeX bloku.
Pravidelný pětiúhelník je na obrázku zde https://www.vypocitejto.cz/obsah-obvod/petiuhelnik/ . Tam uvedené vzorce ale nejsou vhodné pro výpočty ve škole.
V obrázku si vyznač trojúhelník ABS, úhel při vrcholu S má velikost \( 360^\circ : 5 = 72^\circ \). Pravidelný pětiúhelník se skládá z pěti stejných trojúhelníků.
Potřebujeme vypočítat výšku trojúhelníku ABS (\( v_a \)), což je zároveň poloměr kružnice vepsané (na obr. vyznačený \( r_v \)). Použijeme funkci tangens nebo kotangens, např. \( \tan 36^\circ=(a/2)/v_a \). Obsah trojúhelníku ABC je \( S=a\cdot v_a/2 \), obsah pětiúhelníku je pětkrát větší.
Poloměr kružnice opsané vypočítáme pomocí Pythagorovy věty nebo některé goniometrické funkce.
Pro Jana Z.: Aha, to se mi ještě nestalo, ale zatím jsem příspěvků moc nenapsal, tak mě to třeba ještě čeká :)