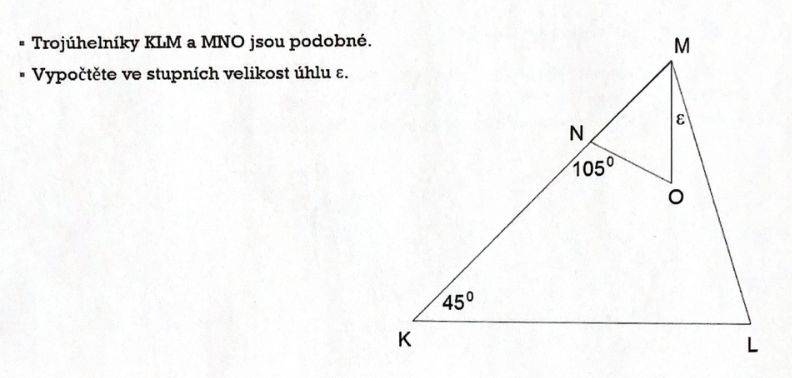
Podobnost trojuhelníků přijímačky SS - dopočítání úhlu

Viz níže

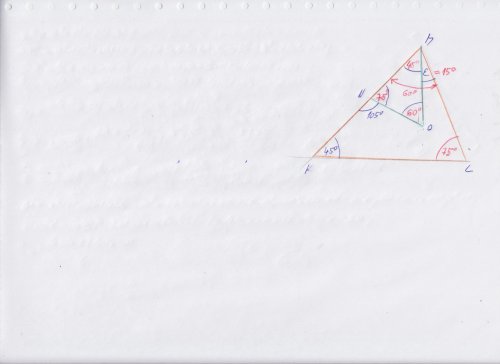
Ahoj Milane, moc děkuju za pomoc, jen prosím porad mi, jak jsi došel k tomu, že je v trojúhelníku MNO v budě "O" uhel 60 stupňů a v bodě M 45 uhel stupňů ? Abych příště věděl jak mám postupovat. Děkuju Rosta

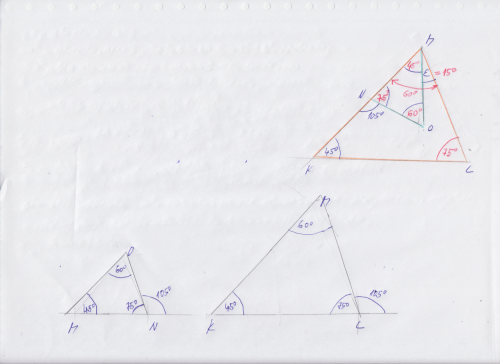
Jen tím způsobem, že jsem uvažoval, že jsou přetočené a protože čistě velikostně vypadal na úhel, který se dá snadno sestrojit, čili graficky sestrojitelný, tak to může být nejčastěji násobek 15° a navíc při vrcholu M je vidět, že celkový je větší než 45 a zároveň menší, než 60°, takže jediné, co pasovalo bylo 45° a ten doplněk tedy 15°. Napovídaly tomu ty použité úhly. Jiné totiž nejdou sestrojit, (tedy jdou ale jen další fermatovské, ale to je běžně nemožné třeba 180°/17, 180°/257 a 180°/ 65537 a samozřejmě jakékoliv jejich poloviny, a dalšího již nikoliv, třeba trisekce nejde udělat, čili 20°, 10° nelze graficky provést. Z tho jsem vycházel.

Takto, kdyby to bylo opravdu přesně to zadání nakreslené, čili oba trojúhelníky vůči sobě v nějakém poměru (nikoliv jen schematicky), tak bych zkusil vzít do kružítka MN a M ztotožnit s K a nanést na KL, podobně do kružítka vzítk MO a nanést od K na KM a pak vzít do kružítka NO a porovnat, zda délkově vyjde stejně, jako z již vynesených koncových bodů na daných stranách KL, KM a pokud v rámci grafické přesnosti ano, je to trojúhelník podobný čili všechny strany ve stejném poměru a tedy i úhly, Tím by se ověřilo (přes délky), že úhel při L a také N je 75°, Prostě já jsem automaticky předpokládal bez přeměřování, že 75°, kteé jsou při vrcholu N jsou také při vrcholu L a tím byla úloha vyřešena , automaticky pak další úhel byl 60° čili při M a při O a doplněk epsilon je jen rozdíl 60° - 45°