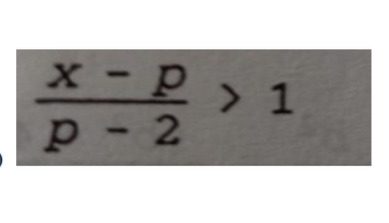Potřeboval bych vypočítat do 18:00!

Přeji pěkný večer, Martine,

bohužel už je po 18:00, nicméně i tak vám zkusím poradit. Předpokládám, že neznámá je zde $x$ a parametr je $p$. Řešíme v $\mathbb{ R}$.

Zadaná nerovnice vypadá následovně:

$\frac{ x-p} { p-2} > 1$

Nejprve musíme stanovit podmínky řešitelnosti. Je zřejmé, že řešení existuje právě tehdy, pokud $p - 2 \neq 0$, tedy $p \neq 2$.

Nyní by bylo vhodné vynásobit celou nerovnici výrazem $p-2$. Toho se ovšem nemůžeme jen tak dopustit, neboť není zřejmé, zda je hodnota tohoto výrazu kladná, nebo záporná.

Rozdělíme výpočet do dvou větví.

1. $p \in (-\infty, 2)$

$\frac{ x-p} { p-2} > 1$

Násobíme výrazem $p-2$, který je záporný, změní se tedy znaménko nerovnosti.

$x-p < p-2$

Upravujeme:

$x < 2p - 2$

2. $p \in (2, \infty)$

$\frac{ x-p} { p-2} > 1$

Násobíme výrazem $p-2$, který je kladný, nezmění se tedy znaménko nerovnosti.

$x-p > p-2$

Upravujeme:

$x > 2p - 2$

Řešení je tedy následující:

pro $p < 2$ platí, že $x \in (-\infty, 2p - 2)$

pro $p = 2$ platí, že $x \in$ { }

pro $p > 2$ platí, že $x \in (2p - 2, \infty)$

Stačí to takto?