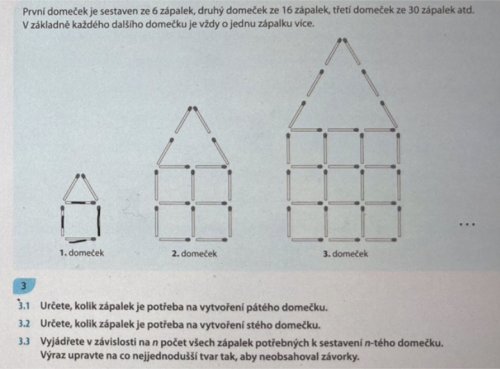
Příklad přijímačky - ntherms

Vážený pane Rostislave,

teď nevím, zda mi jede inernet tak pomalu, že se mi nezobrazuje přiložený obrázek, nebo zda jste jej skutečně zapomněl připojit k příspěvku. Objasníte to?

Posilam obrazek. Dekuji. RN

Přeji pěkné odpoledne, Rostislave,

děkuji za přiložení obrázku.

Začneme jednoduše. Všimněte si, že střecha každého domečku spolu s podkrovím (šikmo nakloněné zápalky a jedna vodorovná řada, která se střechou tvoří trojúhelník) se vždy skládá z trojnásobku zápalek, jaký je "řád" tohoto domečku. Tedy první domeček má střechu ze \(3\) zápalek, druhý z \(6\) zápalek, další z \(9\) zápalek apod.

Z toho plyne, že \(n-tý\) domeček bude mít střechu vytvořenou z \(3 \cdot n\) zápalek.

Co se týče zbytku domečku, je dobré postřehnout fakt, že každý domeček se skládá z konečného počtu pater. Každé toto patro má podlahu (vodorovné sirky) a stěny (svislé sirky).

První domeček má \(1\) patro (jen přízemí, protože podkroví jsme už zahrnuli při výpočtu sirek použitých u střechy). Jejich počet je určen počtem skupin vodorovných sirek. Druhý domeček má \(2\) patra, třetí domeček má \(3\) patra apod. Můžeme tedy říct, že \(n-tý\) domeček má \(n\) pater.

Každé patro se skládá z určitého počtu sirek použitých na vytvoření podlahy a určitého počtu sirek použitých pro vytvoření stěn. Všimněte si, že každé patro má \(n\) sirek použitých pro vybudování podlahy a \(n+1\) sirek pro vybudování stěn. Dohromady je každé patro takto složeno z \(n + n + 1 = 2 \cdot n + 1\) sirek.

Teď to všechno dáme dohromady. Pater je \(n\) a sirek v každém patře \(2 \cdot n + 1\), dům je tedy bez střechy a podkroví tvořen \(n \cdot (2 \cdot n + 1)\) sirkami. Přičteme-li k tomu střechu a podkroví, dostaneme obecný vzorec.

\(a_n = 3 \cdot n + n \cdot (2 \cdot n + 1) = 2 \cdot n^2 + 4 \cdot n \)

Obecný vzorec pro tuto posloupnost je:

\(a_n = 2 \cdot n^2 + 4 \cdot n \),

kde \(n \geq 1\) je 'řád' domečku. Stačí, abyste za \(n\) dosadil čísla z jednotlivých podotázek a máte hotovo.

Mockát Vám děkujeme za pomoc ! R