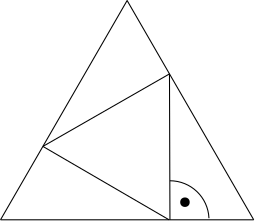
Rovnostranný trojuhelník
Je dán rovnostranný trojuhelník o straně 6cm. Do něho je vepsaný další rovnostranný trojuhelník tak, že jeho vrcholy dělí stranu původního trojuhelníku v poměru 1:2. Stejným způsobem jsou vepsány další trojuhelníky. Určete délku strany desátého trojuhelníku a součet obsahů prvních patnácti trojuhelníků. ( na 2 des. místa v cm´)
Lucie R.
13. 10. 2020 10:56
1 odpověď
Důležité je uvědomit si, že u dělícího bodu je pravý úhel (obrázek). Takže pokud strana prvního trojúhelníka je \(a\), pak (Pythagorova věta), je strana nového trojúhelníka \(a\frac{ \sqrt3} 3\).
Máš tedy geometrickou posloupnost s kvocientem \(q=\frac{ \sqrt3} 3\).
Vypočítat desátý člen by měla být hračka.
Obsah: dva po sobě jdoucí trojúhelníky jsou podobné s koeficientem podobnosti \(q\). Takže jejich obsahy jsou v poměru \(q^2=\frac13\).
Dostáváš opět geometrickou posloupnost obsahů.
Vypočítat součet prvních patnácti členů by opět neměl být problém (samozřejmě, nejdřív si musíš vypočítat obsah prvního trojúhelníka).