Těžká úloha vektory - Střední škola první ročník
Zdravím,
Zdravím,
Můžete mi prosím někdo pomoci s touto úlohou ?
Chtěl jsem si najít souřadnice počátku a konce vektoru, ale nějak se mi to nedaří.
Pomůžete mi prosím.
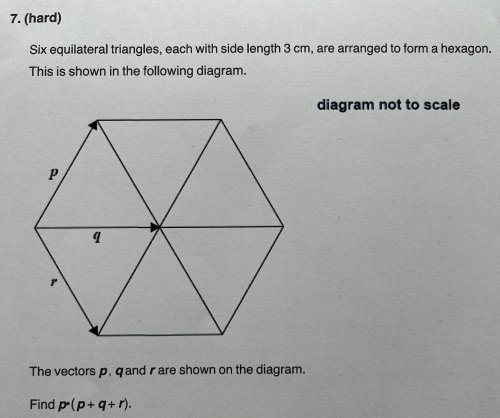
Pokud to neni z obrazu vidět, máme najít řešení : p x ( p+ q + r )
Děkuju Rosta
Rostislav N.
05. 02. 2022 11:07
6 odpovědí
Zdravím,
v pravidelném 6tiúhelníku je \(\vec p+\vec q+\vec r=2\vec q\).
Potom \(\vec p\cdot (\vec p+\vec q+\vec r)=2\vec p\cdot \vec q=2|p|\cdot|q|\cos\alpha=2\cdot3\cdot3\cdot\frac12=9\)
Hallo Zdenek,
dekuji za pomoc ja uz u toho sedim od rana a todle by mne vubec nenapadlo.
Bylo by mozne mi prosim vysvetlit postup, abych podobny priklad priste vyresil sam.
Moc Vam dekuju !
Rosta
Hallo Zdenek,
Muzete mi prosim vysvetlit reseni ?
Moc Vam dekuju !
Rosta
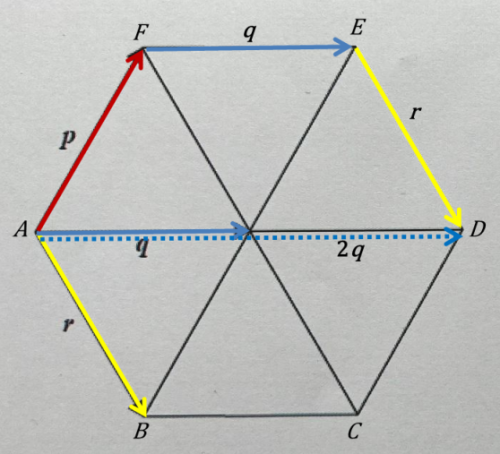
Vektor \( \vec{ p} \) můžeme zapsat
\( \vec{ p} =\vec{ AF} \)
a v geometrii si jej můžeme představit jako posunutí z bodu \( A \) do bodu \( F \) (nebo jiné rovnoběžné posunutí stejným směrem - přesněji orientací - o stejnou délku).
Vektory \( \vec{ p} , \vec{ q} , \vec{ r} \) sečteme takto:
Vektorem \( \vec{ p} \) se "posuneme" z bodu \( A \) do bodu \( F \). Dále přiložíme vektor \(\vec{ q} \), kterým se posuneme z bodu \( F \) do bodu \( E \). Nakonec přidáme vektor \(\vec{ r} \), kterým se posuneme z bodu \( E \) do bodu \( D \).
Ve výsledku jsme se tedy posunuli z bodu \( A \) do bodu \( D \).
Součtem vektorů \( \vec{ p} + \vec{ q} + \vec{ r} \) je tedy vektor \( \vec{ AD} \), což je dvojnásobek vektoru \( \vec{ q} \), tedy \( 2\vec{ q} \).
Zapomněl jsem, že úloha pokračuje :-)
Máme vypočítat
\( \vec{ p} \cdot(\vec{ p} +\vec{ q} +\vec{ r} )=\vec{ p} \cdot(2\vec{ q} ) =2\vec{ p} \cdot\vec{ q} \)
Skalární součin vektorů je definován
\( \vec{ a} \cdot\vec{ b} = |\vec{ a} |\cdot |\vec{ b} |\cdot\cos\alpha\)
\( |\vec{ a} |\) ... velikost vektoru, \( \alpha\) ... úhel mezi vektory, tedy
\( 2\vec{ p} \cdot\vec{ q} = 2|\vec{ p} |\cdot |\vec{ q} |\cdot\cos\alpha=2\cdot 3\cdot 3 \cdot\cos{ 60^{ \circ} } =2\cdot 3\cdot 3 \cdot 0.5=9\)
protože pravidelný šestiúhelník je skládá ze 6 rovnostranných trojúhelníků, jejichž vnitřní úhly měří \( 60^{ \circ} \).
Moc Dekuju Robin, pro mne jako samouka je to skvele vysvetleni !!!! Moc Dekuju za pomoc, R