Vektory

Ahoj,

nevím přesně, co není jasné, tak se prosím ozvi na případné doplnění.

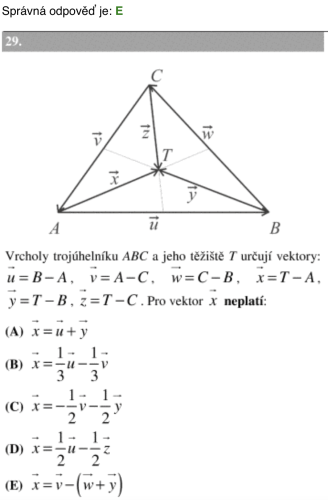
a) Součtem vektorů \( { \vec { AB} } +{ \vec { BT} } ={ \vec { AT} } \), platí tedy \( { \vec u} +{ \vec y} ={ \vec u} \).

b) Vzdálenost těžiště od strany trojúhelníku se rovná třetině výšky k této straně. Rozdělíme-li výšku ke straně trojúhelníku na třetiny a těmito body vedeme rovnoběžky s touto stranou, rozdělí tyto rovnoběžky zbývající strany trojúhelníku na třetiny (podobnost trojúhelníků). Vyznačíme-li na úsečce \( AB \) bod \( Q \) takový, že pro vzdálenost platí \( AQ = AB/3\) , pak \( { \vec { AQ} } ={ \vec u} /3 \) a \( { \vec { QT} } =-{ \vec v} /3 \). Součet vektorů \( { \vec { AQ} } +{ \vec { QT} } ={ \vec { AT} } ={ \vec x} \).

c) Označíme-li střed strany \( AC \) jako \( S \), vektor \( { \vec { AS} } =-{ \vec v} /2 \). Těžiště dělí těžnici na dvě části v poměru 2 : 1, proto \( { \vec { TS} } ={ \vec y} /2 \) a \( { \vec { ST} } =-{ \vec y} /2 \). Platí \( { \vec { AS} } +{ \vec { ST} } ={ \vec { AT} } ={ \vec x} \).

d) Podobně jako c).

e) Tato rovnice není správná, přesvědčíme se o tom složením vektorů.

a) oprava: \( { \vec u} +{ \vec y} ={ \vec x} \)

Moc děkuji za vysvětlení