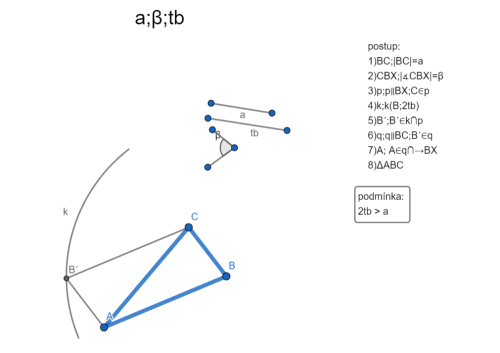
A, ß, tb
Dobrý den, mám dotaz ohledně konstrukce trojúhelníku, Říkáme tomu eukleidovsky příklady. Zde je příklad: strana a, úhel beta, těznice na stranu b. Vzdálenosti si můžeme určit sami. Musím udělat 3 trojúhelníky, kdy začnu vždycky jinou vzdáleností. Mám vyřešený už první dva případy, kde začnu stranou a a betou, ale nevím si rady jak začít s těžnicí. Kdybych začal s betou, tak je to asi přibližně stejně jako když začnu se stranou a (příloha) :
- uhel XBZ 2)BC 3)p || BZ & C ∈ p
- k(B,2tb) 4)B' ∈ p prunik k
- o osa B'B 6)S ∈ osa prunik B,B'
- A ∈ -> CS prunik BX
Docela jsem si tim jisty, ale nenapadá mě vůbec jak začít s těžnicí. Kdyby někdo věděl jak, byl bych moc rád za radu. Děkuji mockrát.
František J.
30. 05. 2023 15:47
3 odpovědi
Z nějakého důvodu se asi nepřipojila příloha a nevypsal se celý postup:
- uhel XBZ 2)BC 3)p || BZ & C ∈ p
- k(B,2tb) 4)B' ∈ p prunik k
- o osa B'B 6)S ∈ osa prunik B,B'
- A ∈ -> CS prunik BX
Děkuji
Ahoj,
konstrukce vychází ze znalosti, že součet sousedních úhlů v rovnoběžníku je 180 stupňů.
-
Narýsuju čáru \(BSB'\), kde \(|BS| = |SB'| = t_b\).
-
Kružnice \(k(B',a)\)
-
Množina všech bodů, ze kterých je úsečka \(BB'\) vidět pod úhlem \(180^\circ-\beta\)
-
Na průsečíku 2) a 3) je bod \(A\).
-
Bod \(C\) je středově souměrný s \(A\) podle \(S\).
Množinou všech bodů, ze kterých je úsečka vidět pod daným úhlem je dvojice oblouků. Jejich středy leží na ose dané úsečky symetricky každý na jedné straně. Středy také leží na přímce, která prochází koncovým bodem úsečky a svírá s ní úhel \(90^\circ - \text{ daný úhel} \).
Pokud je daný úhel větší než pravý, je to ten kratší oblouk, pokud je menší než pravý, je to ten delší oblouk.
Je to jistě důmyslná grafická konstrukce, ale vlastně se nedělá nic jiného, něž že se graficky řeší totéž, co výpočtem, kterým by se to stejně musilo udělat, pokud bychom tohle chtěli realizovat ve velkém měřítku, třeba v neprostupném terénu či v podzemí.
