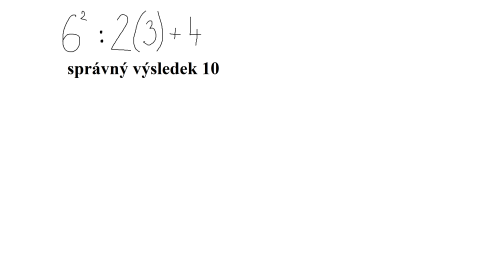BODMAS

Ideální by bylo, kdyby se ten výraz napsal jak se patří, tj, co bylo opravdu zamýšleno, čili jako "ručně" na papíře. Pak nebudou žádné dohady a vyjde co má. Nebo, pokud to má být psáno jako "řádkově", tak důsledně původní výraz závorkovat, jinak je to o ničem.

V přiloženém souboru je zadání a správný výsledek

Tak to je právě to, že takto by se to nikdy "řádkově" zapisovat nemělo a z toho jsou ty umělé "dohady" , co bylo vlastně zamýšleno. Vždy by se měl výraz nejprve jednoznačně zapsat nikoliv řádkově, čili matematicky a pak přepsat řádkově pomocí závorek.

viz níže:

Zkrátka, jednoznačně psáno řádkově to prostě bez závorek nejde. A vymýšlet umělá "pravidla", je zbytečné, dá se jich vyrobit spousta a má to význam leda pro určité kalkulačky (ale i u nich se dá důsledně závorkovat), ale řádkově to psát takto je k ničemu, když stačí psát důsledně závorky. Pak to sedí vždycky, pravda, je to trochu pracné.

Tak některé kalkulačky (kdysi dávno třeba HP) měly např. tzv. reverse polish notation (z určitých důvodů), což byla také vlastně taková podobná umělá pravidla (zadalo se např. 3 enter 4 * a vyšlo 12) jenže "jiná" než BODMAS. A takových umělých se dá vymyslit spousta. Takže tento způsob řádkového zápisu nikdy nepoužívat a nebýt pohodlný psát závorky.

Omlouvám se. Vím, že je to pravda. Totéž, co Vy, jsem psal těm Angličanům.

Já jsem chtěl vědět, zda pravidlo BODMAS nebo PEMDAS je správně použito, že 6*6 : 2(3)+4= 36:6+4=10

Protože oni mi tvrdili, že je to správně, že 66 : 2(3)+4= 36:6+4=10 . Pochopil jsem, že nejspíše rozlišují mezi 66:2(3)+4 a 6*6 :2x(3) +4.: Posílám jejich odpověď. Děkuji za odpovědi

Omlouvám se. Já vím, že je to pravda, co píšete. Totéž jsem psal těm Angličanům. Mně se hlavně jednalo o to, zda je to pravidlo správně použito, o kterém mi tvrdili, že na sedí na ten příklad. Pochopil jsem, že rozlišují mezi 6x6 : 2(3) +4=6x6 : (2(3)) +4=10 a 6x6 : 2x(3) +4=58. Posílám jejich odpověď, ve které tvrdí, že použili pravidlo PEMDAS. Děkuji za odpovědi.

Omlouvám se. Já vím, že je to správně, co píšete. Totéž jsem psal těm Angličanům. Mně se jednalo hlavně o to, zda použili pravidlo PEMDAS správně. Pochopil jsem, že rozlišují mezi 6 x 6 : 2(3) +4 = 36 : (2(3)) +4= 10 a 6 x 6 :2 x (3) +4=58. Posílám jejich odpověď, kde tvrdí, že použili pravidlo PEMDAS správně. Děkuji za odpovědi. Nedaří se mi odeslat obrázek. snad to nyní už dopadne.

Obrázek odešel, ale text je v pořádku, až ten poslední

Tady asi záleží na tom, jak je vnímáno, když tam není explicitně žádný operátor uveden (mezi 2(3)).

V matematice se běžně uvažuje, že to znamená "dopiš si tam násobení".

Oni to sice berou jako násobení, ale ještě k tomu dávají "krom toho násobení si ještě kolem okolních členů dopiš závorky".

Mám zkušenosti s autory vědeckých článků ze všech koutů světa a nikde jsem ten jejich formalismus v praxi neviděl. Pravidlo PEDMAS jste oba použili správně, pouze se liší, jak píšeš, vaše interpretacetoho "explicitně neuvedeného operátoru".

Správný výsledek je 58.

Dělení je první operací. Postupujeme zleva.

Podobnými příklady je internet zaplavený.

Opravdu nechápu ty polemiky.

Chlapci z Anglie sice tvrdí, že tam žádný operátor násobení mezi B a (C+D) není, ale pak to nějak zázračně nahradí (BC+BD); to skoro vypadá, že to mezi sebou vynásobili ne? :D "The guiding operator is Parantheses" se samozřejmě týká jen toho, co je těmi závorkami uzavřeno.

Já bych se jich zeptal, co by řekli na takové \( B(C+D)^2 \). Že by \( (BC+BD)^2 \) ? :-)