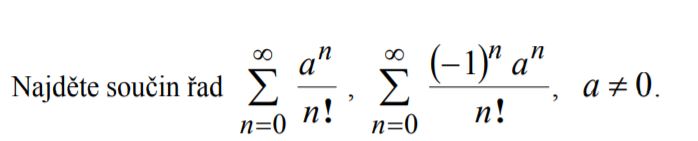Cauchyův součin

Ahoj Petře,

u obou řad, které násobíš, bys měl uhádnout výsledek i o půlnoci, protože jejich součet je \( e \) a \( \frac{ 1} { e} \) , takže součin musí vyjít 1.

Na výpočet komponent jdeš správně, ale na zkoušce tě za ten postup musí vyhodit:

• proč místo rovnítka používáš konvergenci?

• proč rovnou nepoužiješ binomickou větu místo podivného rozkladu [1 + (-1)^n]?

\( c_n = \frac{ 1} { n!} \sum_{ k=0} ^{ n} \binom{ n} { k} (-1)^{ n-k} =\frac{ (1-1)^n} { n!} \)

Všechny členy vyjdou 0 s výjimkou nultého, kde musíš dořešit \( 0^0=1 \)

Aháá, díky

Pro c0 mi vyšla 1, dále pro 1 až n mi vyšla 0. (viz poslední řádek, co píšete).

Součtem součinu je tedy 1. (Když opomenu ten první odstavec, že se ten součet obou řad dá odhadnout), co mi z toho výpočtu říká, že je ten součet součinu roven jedné? Ta jednička pro c0?

Mám tu ještě jeden podobný příklad, kde mám najít součin řad. (viz. foto)

Když to udělám obdobně, tak pro nulu dostanu 1, pro zbytek zase nuly.

V čem je tedy ten rozdíl, když chci určit součet součinu a nebo součin (jako v tomto případě)?

Spíš než odhadnout ... je to asi nejznámější vzorec, co v analýze máme :) \( \sum_{ k=0} ^{ \infty} \frac{ x^k} { k!} =e^x \)

Tím pádem řešení druhého zadání je poměrně jasné, ne?

A když mám součet členů řady Cn, kde nultý člen je 1 a zbylé jsou 0, tak součet musí být 1, není v tom žádná věda.

Ano, tamto je mi jasné, zase to vyjde 1.

Jen mi dělá zmatek, co vlastně mám počítat. V prvním případě součet součinu řad a v druhém součin řad.

Počítáš pořád to stejné, ale asi jste si moc nevysvětlovali, co je smyslem.

Existuje velká spousta čísel, které nemůžeme vyjádřit uzavřenou analytickou formou. Místo toho jejich hodnotu uvádíme jako nějaký vztah. A řady slouží jako velmi užitečná forma takového vyjádření.

Příkladem je Eulerovo číslo, které má velmi intuitivní definici \( e=\sum_{ n=0} ^{ \infty} \frac{ 1} { n!} \)

Takže se musíš koukat na řady jako na matematický objekt určitého druhu, jinými slovy ber řadu jako číslo.

Až budeš mít trochu víc znalostí z abstraktní a lineární algebry nebo teorie množin, tak uvidíš, že řada je opravdu číslo v celém tom smyslu, jak ho chápeš teď.

Když máš dvě řady (čísla), můžeš je sečíst (stejně jako čísla) nebo vynásobit (stejně jako čísla).

A výsledek chceš znát opět ve formě řady, třeba proto, že uzavřená forma zase nemusí existovat.

Cauchyův součin využívá důležité vlastnosti spočetných množin, matematické indukce, a dává jednoduchý návod, jak součin dvou řad zapsat zase jako řadu.

Popravdě, to už jsme ani nějak neprobíraly, přednášky zrušené..

Díky, no snad se tím prokoušu.