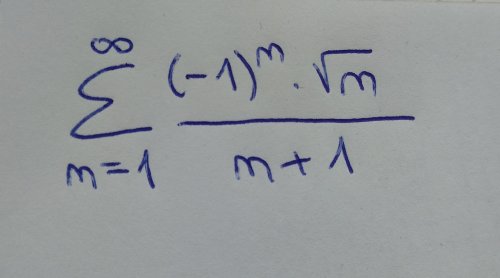Konvergence alternující řady
Zdravím, měla bych dotaz ohledně konvergence této alternující řady. Úkolem je ověřit nutnou podmínku konvergence a dále určit, zda tato řada konverguje absolutně/relativně či diverguje užitím vhodného kritéria konvergence.
Eva Š.
06. 05. 2021 16:07
4 odpovědi
Ahoj Evo. Konverguje to, ale ne absolutne. Je to alternujici rada a limita te casti bez alternace je nula. Cili konverguje. Ale klesa prilis pomalu. Kdyz odstranis tu alternaci, chova se to jako odmocnina z n lomeno n. Divergenci muzes budto dokazat primo integralnim kriteriem nebo treba srovnavacim kriteriem, kdy to zdola odhadne radou 1/n, o ktere se obecne vi, ze diverguje. Pripadne jeji divergentnost ukazes taky integralnim kriteriem.
Marek
No já se právě zasekla hned na začátku, kdy ověřuji nutnou podmínku konvergence. Tudíž odstraním alternaci a zbytek se má rovnat nule. Ale když mám ten zbylý výraz odmocnina z n lomeno n plus jedna, tudíž po dosazení výraz nekonečno lomeno nekonečno, tak jak ten výraz musím upravit, aby vyšla požadovaná nula?
Vytkni si ve jmenovateli n, pokrat to s odmocninou a posli do nekonecna. Je to v podstate limita polynom lomeno polynom. Mam na to videa. Zadej do vyhledavace tady na Mathematicatoru limita. Vypadnou na tebe videjka.
Moc děkuji za radu, podívám se na videa