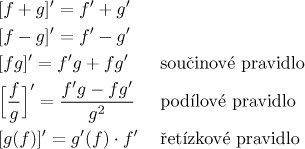Diferenciální rovnice 2. řádu

Zřejmě je, podívám se a když tak napíši a samozřejmě že na lineární diferenciální rovnice jakéhokoliv řádu lze používat řešení s pomocí Wronskiánu alias determinantu Wronského. Tak ona i prvního řádu je to fakticky toto řešení, jen se to tak nenazývá (protože ten Wronskián je prvního stupně, čili přímo ten člen), nazývá se variace konstanty, (kdy z

c -> c(x) ) ale to se dělá i zde. Jen pak začne být problém s řešením charakteristické algebraické rovnice, protože od 5. stupně a více, sice mohou mít i řešení v konečném počtu algebraických výrazů ale obecně ne, prostě jen tak ad hoc zapsaná LDR rovnice 5. stupně obecně nikoliv, ale v určitých případech také. Prostě do 4. stupně jsou jednotlivé kořeny té rovnice vyjadřitelné pomocí koeficientů u členů jednotlivých stupňů, od 5. občas ano ale většinou ne, souvisí to s fermatovskými prvočísly.

Díky Milane!

No my probíráme jen rovnice (I. a) II. řádu, a ten Wronski mi přijde srozumitelný a univerzální

Tak mne zajímalo, zda když v testu budu mít zadáno y′′ ... nebudu to mít špatně s Wronskim

Určitě ne, ale ten příklad asi přeci jen budete musit opravit, v tom W ( x ) je ten člen w22 = e ^ x + x * e ^ x = e ^ x ( x+1 ) , když to vynásobíte tím w11 = e ^ x , dostanete e ^ x * e ^ x ( x + 1 ) = e ^ 2 x ( x + 1 ) = x * e ^ 2 x + e ^ 2 x . O toho odečtete ten x * e ^ x * e ^ x a zbyde e ^ 2 x . To pak v podílu W1 ( x ) / W ( x) udělá, že bude - x^3 / e ^ x = - x ^ 3 * e ^ - x a to se dá upravit po částech a dost se to rozšíří.

Zkontrolovat to, že to je dobře můžete poté tak, že dosadíte ten V(x) tzv. partikulární integrál do té původní rovnice ( co máte v zadání ) a musí vyjít, že levá strana = pravá strana

Jasně, takže chyba v derivaci součinu fcí

Tady to máte přepočtené

k tomu 1 ) str. 2 ) :

řešení pomocí Wronského determinatů je vlastně také metoda variace konstant, z těch C 1 , C 2 vznikne C 1 ( x ) + K 1 , C 2 = C 2 ( x ) + K 2 a pak se obě tyhle nové funkce i nové konstanty přenásobí tím fundamentálním systémem y 1 ( x ) = x , y 2 ( x ) = x * e ^ x a dostane se tím obecné řešení, kde ta "druhá" část se násobí C 1 ( x ) * y 1 ( x ) , C 2 ( x ) * y 2 ( x ) a to je ten partikulární integrál, který můžeme zkontrolovat derivací a dosazením do té původní rovnice

Díky moc, jdu si to projít!