Eukleidova věta nevím si rady

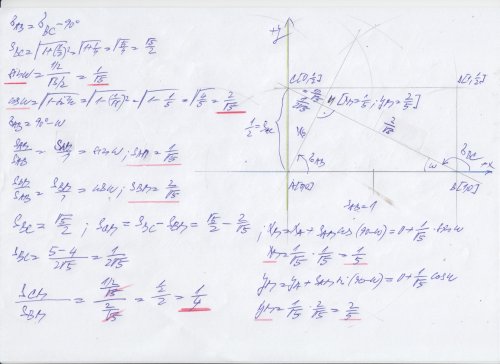
Viz níže, opravdu žádnou Eukleidovu větu netřeba, stačí uvažovat, jaké jsou úhly při těch vrcholech v tom trojúhelníku ABM a pak si je vyjádřit, totiž jejich funkce (úhly jako takové ve stupních nepotřebujeme, jen algebraicky jejich funkce sin omega, cos omega) a pak spočíst snadno (známe základnu a oba úhly co se doplňují na 90° ) z toho ty jednotlivé úseky, tedy, stačí jeden, druhý odečteme od celé délky a pak poměr je evidentní, alias 1 : 4, máte to pro kontrolu navíc v souřadnicích. Takhle by se to dělalo v technické praxi, (zde je položené a = 1, jde jen o poměry a to "a" samotné není třeba). Čili fakticky je ten poměr dán poměrem S(AM) : S(BM) = ( 1 / 2 ) * sin omega / cos omega = 1 / 4 , kde omega je zde úhel při vrcholu B

čili poměr je ( 1 / 2 ) * tg omega = 1 / 4

V obecném případě, kdy S(AB) = a délkových jednotek , S(BD) = b délkových jednotek , pak poměr S ( DM ) : S ( BM ) = b ^ 2 : a ^ 2 , nebo po úpravě také S ( DM ) : S ( BM )= ( b / a ) ^ 2 tedy poměr druhých mocnin délek stran , nebo také poměr stran povýšený na druhou